転置インデックスの圧縮技法

Takuya Asano

Oct 23, 2022 • 28 min read

転置インデックスは、検索エンジンの実装において、中心的な役割を果たすデータ構造である。

転置インデックスのデータ構造とアルゴリズムは、クエリ処理アルゴリズムとともに、検索エンジンの性能に直結する。とくに大規模な検索エンジンにおいては、キャッシュ効率を高めてクエリ処理を高速化するために、転置インデックスの圧縮は必要不可欠となっている。

この記事では、転置インデックス、とくにポスティングリストの圧縮について、近年の手法を簡単にまとめる。

転置インデックスの基本
- 転置インデックスのデータ構造と特性
- 転置インデックスのアクセスパターン
近年のインデックス圧縮技法
- Variable-Byte Family
- Simple Family
  - Simple9
  - Simple16
  - Simple8b
  - QMX
- PFor Family
- Elias-Fano Family
  - Elias-Fano
  - PEF
  - Roaring
  - Slicing
- Binary Interpolative
  - BIC
- Directly-Addressable
  - DAC
- Dictionary-based
  - DINT
- Bitmap Compression
  - BBC
  - WAH
  - EWAH
  - CONCISE
  - PLWAH
  - VALWAH
  - SBH
実装とベンチマーク
参考文献

転置インデックスの基本

具体的なポスティングリストの圧縮技法について触れる前に、転置インデックスの基本について、ざっくりと説明する。

転置インデックスのデータ構造と特性

転置インデックス (inverted index) は、ターム辞書 (term dictionary) とポスティングリスト (posting lists) （転置リスト (inverted list) とも）から構成される。

転置インデックスは以下のような構造をもち、ターム (term) とポスティングリストが一対一で対応している。

Christopher D. Manning, Prabhakar Raghavan, and Hinrich Schütze. 2008. Introduction to Information Retrieval. Cambridge University Press, USA. — Christopher D. Manning, Prabhakar Raghavan, and Hinrich Schütze. 2008. Introduction to Information Retrieval. p.7 Figure 1.3

ポスティングリストの各要素のことを、ポスティング (posting) といい、そのタームが含まれる文書 ID を意味している。たとえば上記の例では、文書 2, 31, 54, 101 に Calpurnia というタームが含まれている。

ポスティングリストは、以下のような特徴をもっている。

非負の整数のみが含まれる
同じ数は含まれない
単調増加数列（ソートされている）
コレクション（文書集合）によるが、値の分布は偏っていることが多い

多くの技法がこれらの特性をうまく使って、効率的な圧縮を実現している。

転置インデックスのアクセスパターン

検索クエリ処理において、ポスティングリストは基本、シーケンシャルに（前から順番に）アクセスされる。

ただし、AND クエリ (conjunction query, intersection) などの、複数のポスティングリストをまたぐクエリ処理では、効率化のため、いずれかのポスティングのカーソルを特定の文書 ID までスキップするという最適化が行われる。

OR クエリ (disjunction query, union) においても、MaxScore や WAND などの枝刈り (pruning) アルゴリズムにより、このようなスキップが積極的に行われる。

近年のインデックス圧縮技法

Techniques for Inverted Index Compression というサーベイ論文にて、2019年までの整数（列）圧縮技法が調査されている [Pibiri&Venturini21]。

Giulio Ermanno Pibiri and Rossano Venturini. 2020. Techniques for Inverted Index Compression. Table 1

また、 An Experimental Study of Bitmap Compression vs. Inverted List Compression では、 bitmap compression と呼ばれる手法群と、整数列圧縮技法との比較がなされている [Wang+17]。

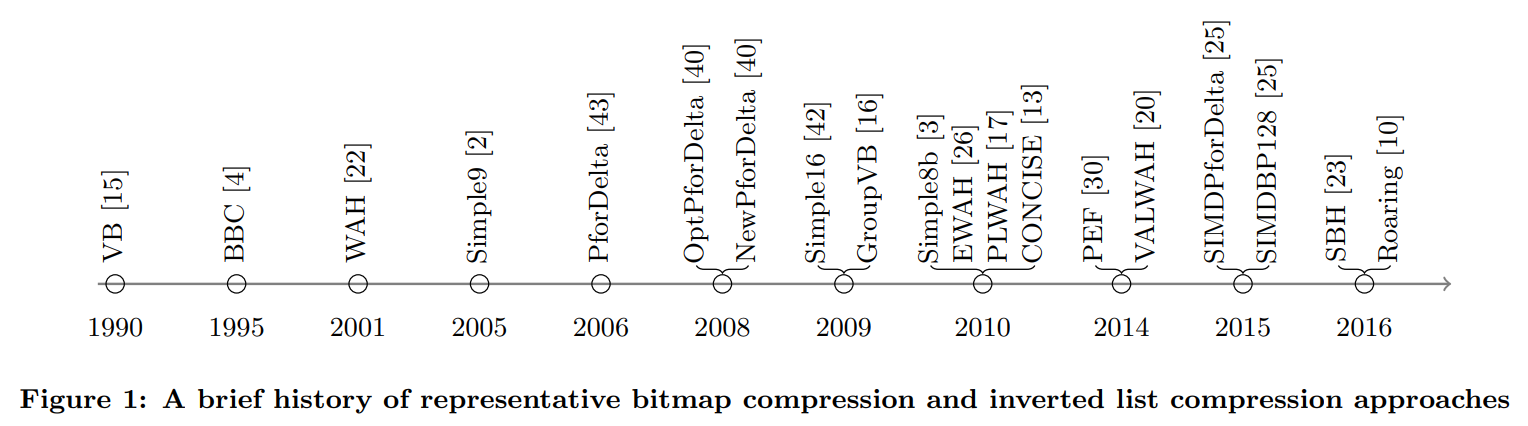
Jianguo Wang, Chunbin Lin, Yannis Papakonstantinou, and Steven Swanson. 2017. An Experimental Study of Bitmap Compression vs. Inverted List Compression. Figure 1

以下では、それぞれの圧縮技法について、簡単に紹介する。

Variable-Byte Family

整数値をそれぞれ圧縮
ビットではなくバイト単位に揃える (byte-aligned)
SIMD が使えるので高速化しやすい

VByte (Variable-Byte) [Thiel&Heaps72]

整数値をバイトの並びにする
- 1 byte は 1 bit のコントロールビットと 7 bit のデータビットで表現
最初のバイトのみコントロールビットを 0 にする
- 続いているバイトではコントロールビットは 1
たとえば、 65790 は 00000100.10000001.11111110 となる
デコードするときはデータビットを連結
大きい整数値のときには効率的

参考

Information Retrieval: Implementing and Evaluating Search Engines 6.3.4, 6.6
下記の講義スライド p.16

Varint-GB [Dean09]

バイト単位 (byte-aligned) なのは同じ
最初の 2 bit を長さを表現するのに使う
4つの整数値ごとにグルーピング
- グループごとの 2 bit を集めて、 8 bit のタグを作る
- タグを見れば 4 つの整数値をそれぞれどの長さでデコードすればよいかわかる
デコードが Variable-Byte より高速
- 従来の Variable-Byte は ~180M numbers/sec
- Varint-GB は ~400M numbers/sec
Google の転置インデックスのフォーマットに採用された
Varint-GB と呼ばれている
- Group varint で、長さのエンコードは binary (not unary)

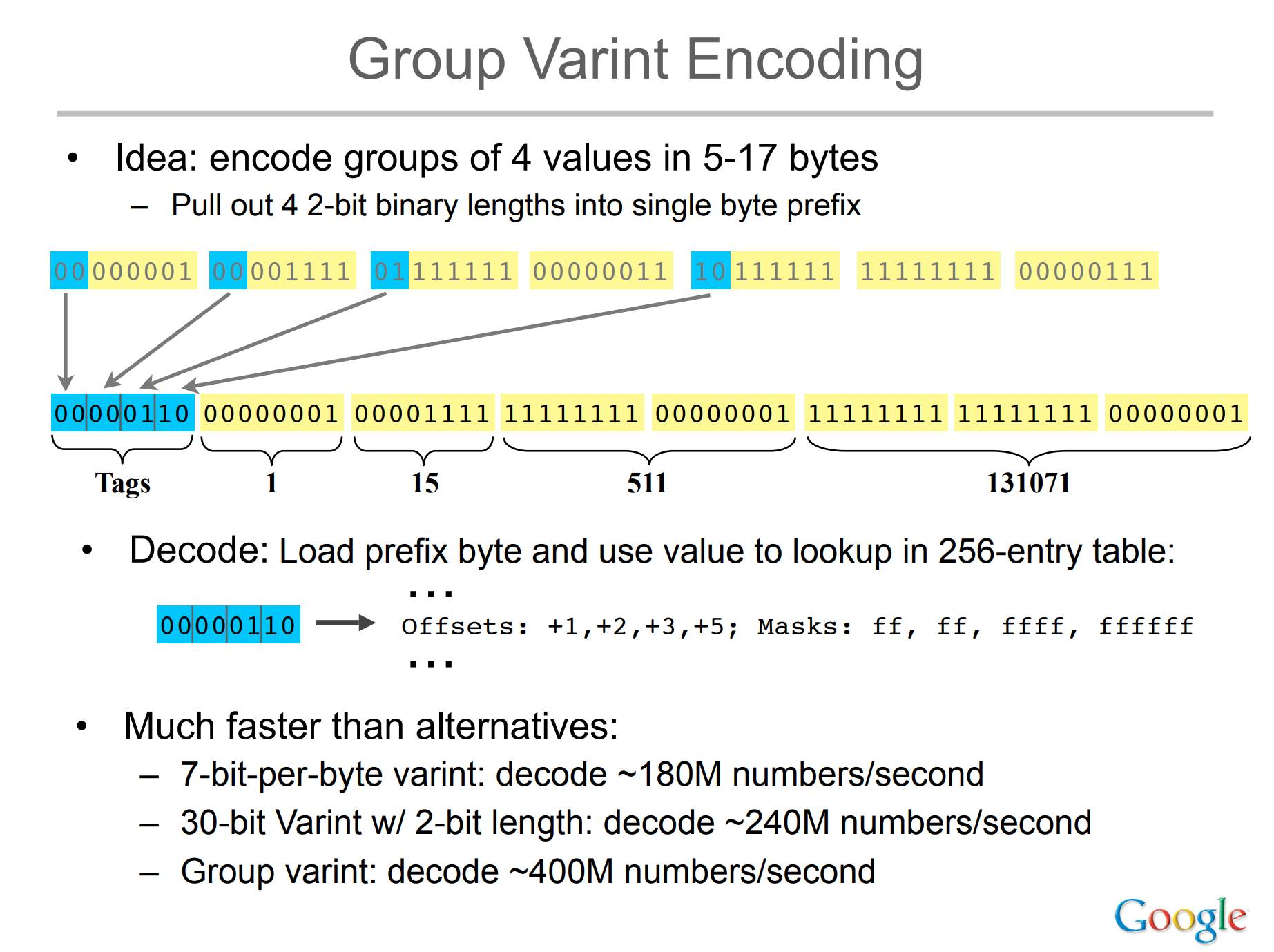
Jeffrey Dean. 2009. Challenges in building large-scale information retrieval systems: invited talk p.63

参考

下記のスライド pp.55-63

Varint-G8IU [Stepanov+11]

SIMD 命令でデコードをベクトル化
Varint-GB と同じようにグループごとに 1 byte のコントロールバイト（タグ）を使う
ひとつのグループの中に 2 から 8 の整数を入れられる
- 固定サイズ (e.g., 8 bytes) のブロックにできるだけ多くの整数を詰め込む
- 固定サイズであることで SIMD と相性がいい
Amazon の Stepanov によって開発された
- 特許が取られている

Alexander Stepanov, Anil Gangolli, Daniel Rose, Ryan Ernst, and Paramjit Oberoi. 2011. SIMD-based decoding of posting lists. Figure 3

Alexander Stepanov, Anil Gangolli, Daniel Rose, Ryan Ernst, and Paramjit Oberoi. 2011. SIMD-based decoding of posting lists. Figure 5

参考

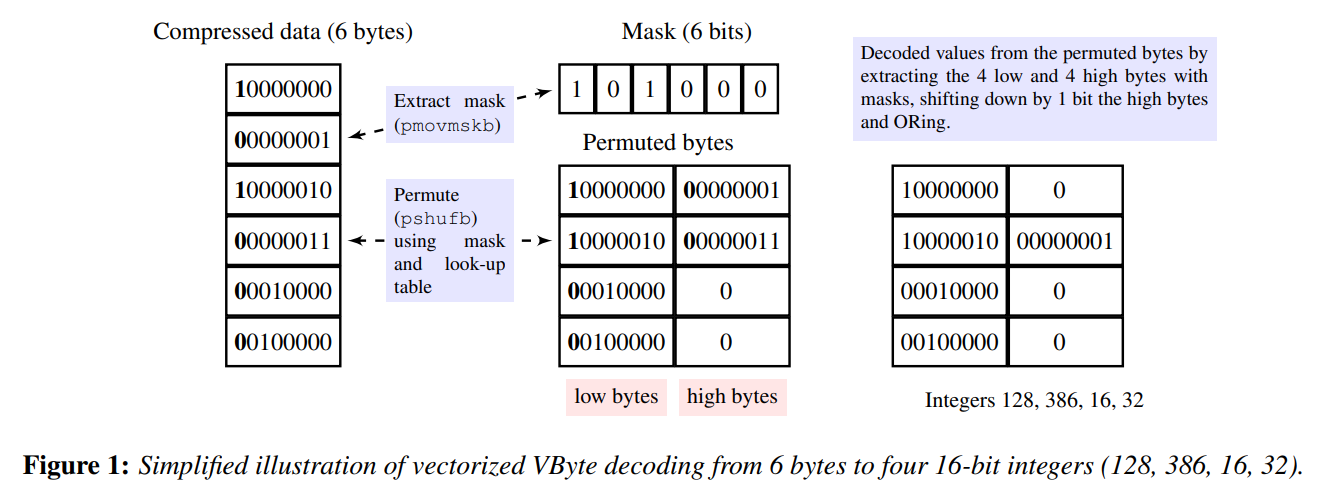
Masked-VByte [Plaisance+15]

同じく VByte の SIMD 実装
フォーマットはオリジナルの Variable-Byte と同じ
デコード
- 専用の SIMD 命令を使って、最初に MSBs (most significant bits) を集める
- 事前に構築されたルックアップテーブルとシャッフル命令を使って整数に変換する
オリジナルの VByte よりは速いが、 Varint-G8IU よりは遅い
- ただし、 Varint-G8IU と違ってパテントフリー
Indeed の Jeff Plaisance によって開発された

Vectorized VByte Decoding

We consider the ubiquitous technique of VByte compression, which representseach integer as a variable length sequence of bytes. The low 7 bits of eachbyte encode a portion of the integer, and the high bit of each byte is reservedas a continuation flag. This flag is set to 1 for all bytes except t…

arXiv.orgJeff Plaisance

実装

https://maskedvbyte.org/ から C/C++ 実装がダウンロード可能

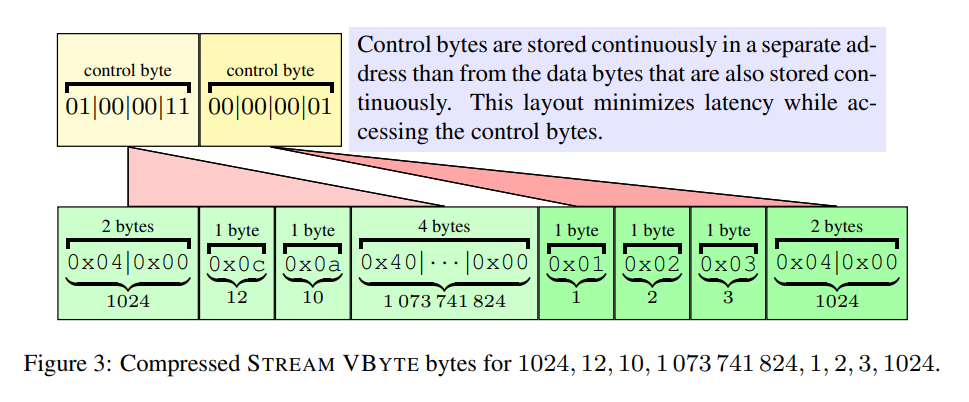
Stream-VByte [Lemire+18]

SIMD で高速なデコードを達成
Varint-GB は制御バイトとデータバイトがインターリーブで保存されているので、SIMD による並行処理が難しかった
- 可変長なので、前のグループの制御バイトをデコードしないと次のグループがどこに保存されているのかわからない
- このデータの依存関係により、並列化しようとしてもCPUが遊んでしまう
制御ビットとデータビットを別の場所に保存することで CPU にデータを供給しつづけることができる
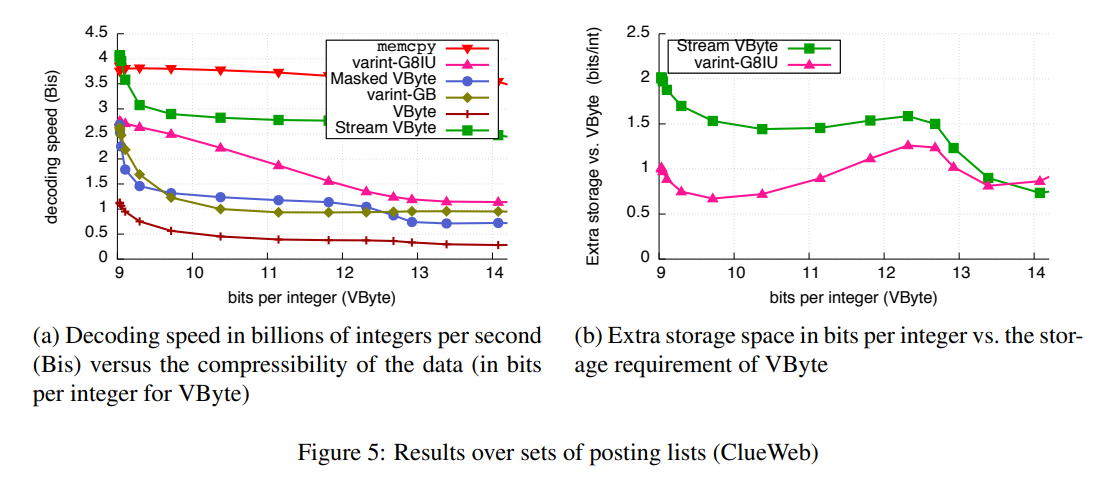
Varint-G8IU よりデコードが最大で2倍高速
- 条件によっては memcpy を超える速度

Stream VByte: Faster Byte-Oriented Integer Compression

Arrays of integers are often compressed in search engines. Though there aremany ways to compress integers, we are interested in the popular byte-orientedinteger compression techniques (e.g., VByte or Google’s Varint-GB). They areappealing due to their simplicity and engineering convenience. Amazo…

arXiv.orgDaniel Lemire

実装

Opt-VByte [Pibiri&Venturini20]

複数の可変長のブロックに分割
密なブロックはビットベクトルで、疎なブロックは VByte でエンコードする
- Cardinality によるパーティショニング
- PEF と同じアプローチ
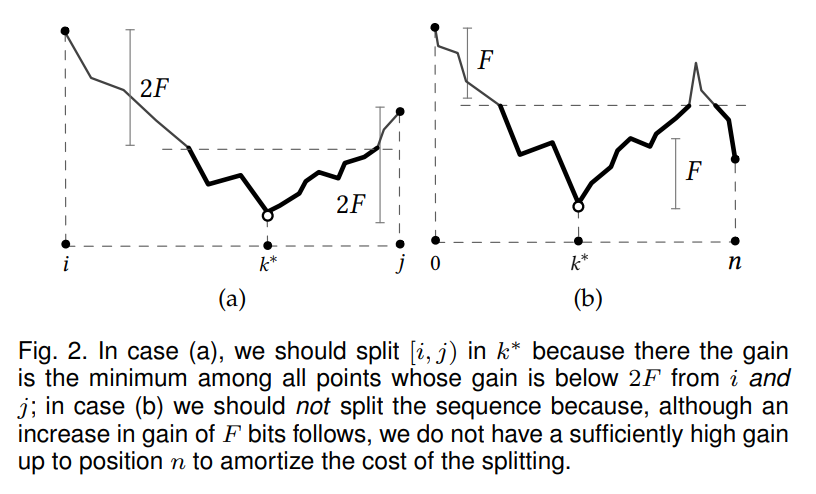
ブロックの選び方を最適化する
- 最適な分割を時間計算量 Θ(n)、空間計算量 O(1) で厳密解を見つけられる
- 定数係数は非常に小さいので、実際にはかなり高速
- VByte でなくても、 point-wise な整数のエンコーダー（Unary, Golomb, etc）ならなんでも適用可能

Giulio Ermanno Pibiri and Rossano Venturini. 2020. On Optimally Partitioning Variable-Byte Codes. Fig. 2

On Optimally Partitioning Variable-Byte Codes | IEEE Transactions on Knowledge and Data Engineering

The ubiquitous <italic>Variable-Byte</italic> encoding is one of the fastest compressedrepresentation for integer sequences. However, its compression ratio is usually notcompetitive with other more sophisticated encoders, especially when the integers to...

IEEE Transactions on Knowledge and Data EngineeringGiulio Ermanno Pibiri ISTI-CNR and the University of Pisa, Pisa, Italy

https://rossanoventurini.github.io/papers/TKDE20.pdf

実装

Simple Family

Variable-Byte とは違って、ソート済みリストの圧縮に適した手法（PForなどと同様）
リストの要素間の差分 (gap) をエンコードする
複数の差分を 1 word (32 bits - 128 bits) に詰め込む
セレクタによってデータ部分をどうデコードするか（ビットパターン）を決める

Simple9 [Anh&Moffat05]

Simple4b とも呼ばれる
32 bits の中にできるだけ差分 (gap) を詰め込む
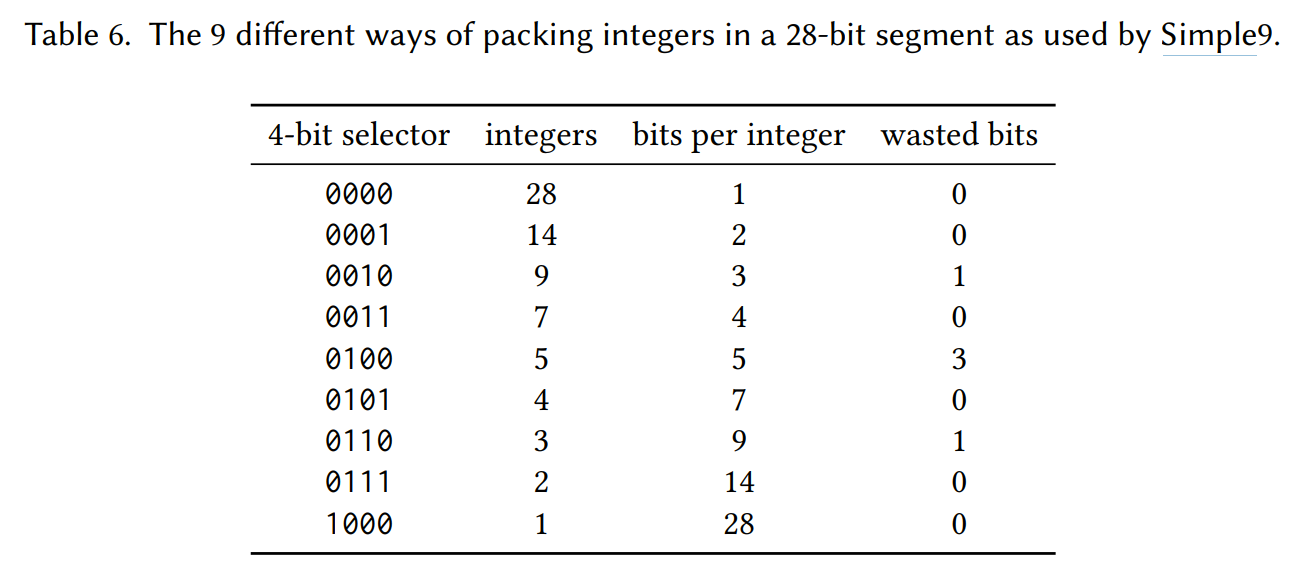
4 bits からなるセレクタと、残りの 28 bits に分ける
全9種類のセレクタによって残りの 28 bits に何個の整数を詰めるかを決める
- たとえば、セレクタが 0000 のときは 1 bit の整数 28 個を詰める
- 0010 のときは 3 bits の整数を 9 個詰める（このとき 1 bit は無駄になる）

Giulio Ermanno Pibiri and Rossano Venturini. 2020. Techniques for Inverted Index Compression. Table 6

Inverted Index Compression Using Word-Aligned Binary Codes | Information Retrieval

We examine index representation techniques for document-based inverted files, andpresent a mechanism for compressing them using word-aligned binary codes. The newapproach allows extremely fast decoding of inverted lists during query processing,while ...

Information RetrievalVo Ngoc Anh Department of Computer Science and Software Engineering, The University of Melbourne, Victoria 3010, Australia

Simple16 [Zhang+08]

Simple9 と同様に、32 bit の中にできるだけ差分 (gap) を詰め込む
4 bits からなるセレクタと、残りの 28 bits に分ける
全16種類のセレクタで、残りの 28 bits にどのように整数を詰めるか（ビットパターン）を決める
- たとえば 5, 5, 5, 5, 4, 4 で合計 28 bits
- Simple9 では無駄なビットがあったが、それがなくなる
- 全ビットパターン: https://github.com/lemire/JavaFastPFOR/blob/1b9f1290edf66ec2b439c5d192a91c187d292812/src/main/java/me/lemire/integercompression/Simple16.java#L174-L182

http://ra.ethz.ch/CDstore/www2008/www2008.org/papers/pdf/p387-zhangA.pdf

Simple8b [Anh&Moffat10]

Simple16 の亜種
32 bits ではなく 64 bits の中に整数を詰める
4 bits のセレクタと、残りの 60 bits に分ける
全14種類のセレクタ

Index compression using 64-bit words | Software—Practice & Experience

Modern computers typically make use of 64-bit words as the fundamental unit of dataaccess. However the decade-long migration from 32-bit architectures has not been reflectedin compression technology, because of a widespread assumption that effective ...

Software—Practice & ExperienceVo Ngoc Anh Department of Computer Science and Software Engineering, The University of Melbourne, Victoria 3010, Australia

QMX [Trotman14]

SIMD 命令を活用
同じく Simple の亜種で、128 bits もしくは 256 bits のなかに整数を詰める
他の Simple とは違い、セレクタ（eXtractors と呼ぶ）とデータ（Quantities と呼ぶ）を別々に保存する
- 別のストリームとすることで CPU が遊ばないようにする
セレクタのストリームはランレングス符号 (RLE) でエンコードされる
- セレクタは 16 種類しかないので、同じものが続きやすいため
- (value, length) のペア
- たとえばセレクタのストリームが [12, 12, 12, 5, 7, 7, 7, 7, 9, 9] だったとき、RLE は [(12, 3), (5, 1), (7, 4), (9, 2)] となる

PFor Family

Patched Frame-of-Reference
Simple と同様に、ソート済みリストの圧縮に適した手法
- リストの要素間の差分 (gap) をエンコードする
ブロック単位でエンコード
ブロック中に大きい差分があると、それを表現するのに必要なビット数が増えるため、スペース効率が悪くなる
ブロック中の大きい差分は別の場所に保存すれば、小さい差分は少ないビット数でエンコードできる
- 実データにおいては、ポスティングリストの差分はほとんどの場合小さい
- たとえば差分が 15 以下なら、各差分は 4 ビットでエンコード可能
- このアプローチを patching と呼ぶ

PForDelta [Zukowski+06]

ブロックごとに2つのパラメータ b と k を選ぶ
- ブロックの中の整数のほとんど (e.g., 90%) が [b, b + 2^k - 1) の範囲に入るようにする
その範囲に入る差分 x は、 x - b を k ビットでエンコードする
k ビットに収まらない、大きい差分は例外 (exception) として別の場所に保存する
たとえば [3, 4, 7, 21, 9, 12, 5, 16, 6, 2, 34] というリストがあったとき、b = 2, k = 4 を選ぶと
- [1, 2, 5, *, 7, 10, 3, *, 4, 0, *] となり（ * は exception）、 exception は [21, 17, 34] となる
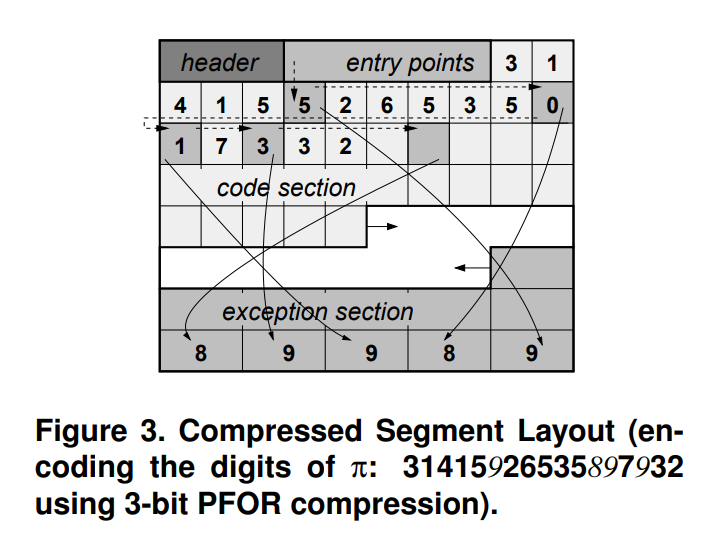
元論文では、ディスク上での各ブロックのレイアウトを以下のように定めている
- header: パラメータ (b, k) の値と、他の領域の開始位置とサイズなどが保存される
- entry point section: 128個ごとに、次の例外の位置と、対応する exception section のオフセットを保存する領域
- code section: それぞれのエンコードされた値を格納する領域
  - 例外の場合には、次の例外へのオフセットが書かれる
  - 次の例外が離れすぎていて k ビットで表現できない場合、例外でない値を適当に選んで例外として扱う必要がある
- exception section: 例外の値を保存する、後ろに向かって伸びる領域
デコードで分岐予測が発生しないので高速

Marcin Zukowski, Sandor Heman, Niels Nes, and Peter Boncz. 2006. Super-Scalar RAM-CPU Cache Compression. Figure 3

https://www.researchgate.net/publication/4234735_Super-scalar_RAM-CPU_cache_compression

NewPFD [Yan+09]

PForDelta + Simple16
例外 (exception) を表現するために、例外のオフセット値と例外を2つの別の配列に保存する
- code section の例外に対応する場所には、例外の下位 b ビットを書く
- 例外の残りのビットを別の配列に書く
- 例外のオフセット（次の例外への位置差分）を別の配列に書く
- この2つの配列を Simple16 でさらに圧縮する

整数列圧縮 from JAVA DM

Opt-PFor [Yan+09]

PForDelta の最適化バージョン
ブロックのサイズが小さくなるように、パラメータ b, k を最適化
PForDelta より小さくなるが、速度は少しだけ落ちる
NewPFD と同じ論文で提唱された

実装

Fast-PFor, SIMDPforDelta, SIMDBP128 [Lemire&Boytsov15]

これも PForDelta の亜種
例外をページ（ブロックのグループ）に圧縮する
- たとえば 1 ページは 32 個のブロックで構成される
- ページごとに例外をまとめて記録する
ページ単位でまとめてデコードすることで高速化
SIMD でさらに高速化できる
- SIMDPforDelta, SIMDBP128

Decoding billions of integers per second through vectorization

In many important applications -- such as search engines and relationaldatabase systems -- data is stored in the form of arrays of integers. Encodingand, most importantly, decoding of these arrays consumes considerable CPU time.Therefore, substantial effort has been made to reduce costs associate…

arXiv.orgDaniel Lemire

実装

Elias-Fano Family

Elias-Fano とその亜種（他の手法と組み合わせたハイブリッドを含む）

Elias-Fano [Elias74, Fano71]

ソート済み整数配列は上位ビットが共有しやすいことに着目
下位ビット（ l ビットとする）と上位ビットを分けて保存する
- 下位ビットはそのまま
- 上位ビットは、同じ上位ビットをもつ組み合わせ（クラスタ）ごとに、そのクラスタの個数を Unary code でエンコードする
- たとえば以下の例では、クラスタの数がそれぞれ 3, 3, 1, 1, 2, 0, 1, 1 なので、上位ビットは 1110.1110.10.10.110.0.10.10 というビットベクトルにエンコードされる

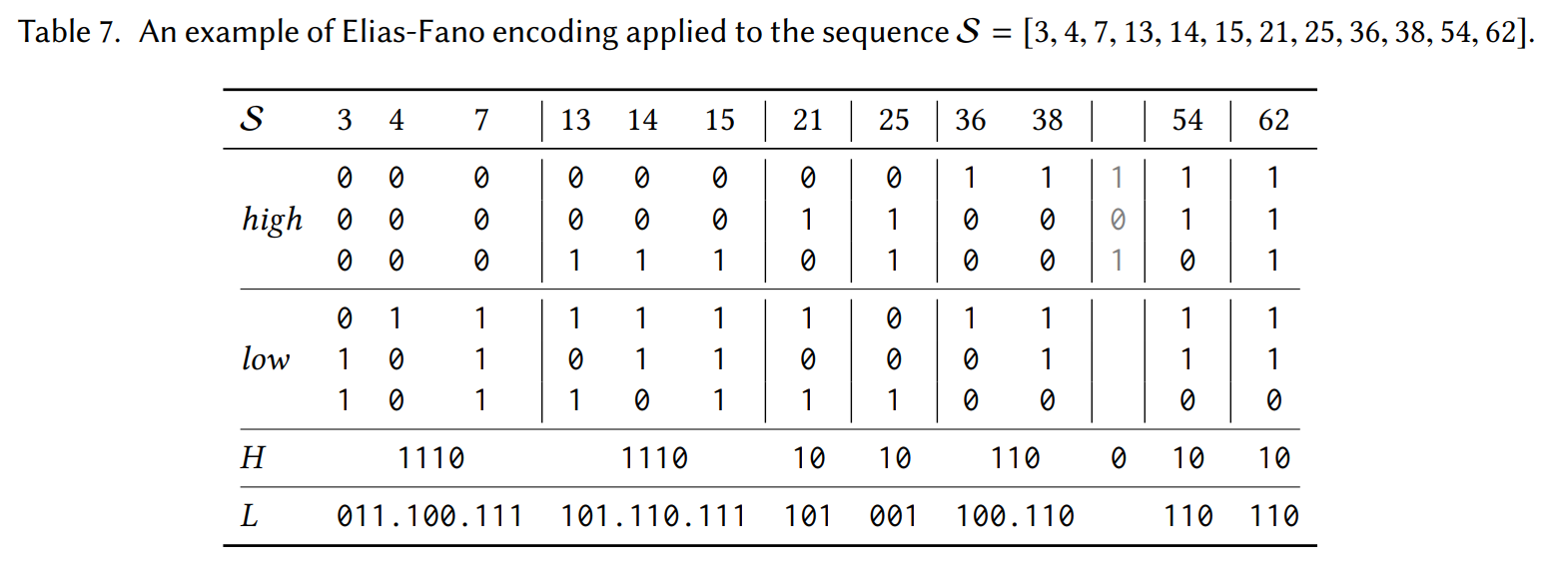
Giulio Ermanno Pibiri and Rossano Venturini. 2020. Techniques for Inverted Index Compression. Table 7

ランダムアクセスが可能
- 下位ビットの配列 ( low_bits ) からのデコードは、単に low_bits[i] でよい
- 上位ビットをエンコードした配列 ( high_bits ) はビットベクトルなので、 Rank 演算と Select 演算を利用できる
- i 番目の要素の上位ビットのデコードは、 Rank0(Select1(i)) を計算すればよい

PEF [Ottaviano&Venturini14]

Partitioned Elias-Fano
Elias-Fano に対して、カーディナリティによるパーティショニングを行う
ソート済み整数列が近くに集まっている場合、それらを密ビットベクトル、いわゆるビットベクトル (characteristic bit-vector) で表現する
- たとえば [2,3,4,5,6,7,10,11,13] は 0111111001101 （左から 1, 2, 3, … を表す）で表現できる
- 整数列が密な場合、ビットベクトル表現もコンパクトになる
疎な整数列の部分に対しては、 Elias-Fano でエンコードする

A Crash Course on Data Compression. 3. List Compressors p.24

Roaring [Chambi+16, Lemire+16, Lemire+18]

Universe （エンコード対象がとりうる整数値の空間）に対するパーティショニングを行う
- PEF のようにカーディナリティによってパーティショニングするのではなく、固定のビット数でパーティショニングする
- たとえば Universe が 2^32 だったとして、上位 16 ビットでパーティショニングすると、空間は 2^16 のチャンクに分割される
各チャンクは、密な場合はビットベクトルでエンコードし、疎な場合は sorted list としてエンコードする
- 疎な場合は、同様にさらに Universe を分割できる
- たとえば、上の例では、 2^16 の Universe をさらに 2^8 に分割できる
カーディナリティによるパーティショニングよりもサイズは大きくなるが、 intersection や union は高速にできる
- すべてのポスティングリストにおいて、空間が同じように分割されているため

A Crash Course on Data Compression. 3. List Compressors p.25

Better bitmap performance with Roaring bitmaps

Bitmap indexes are commonly used in databases and search engines. Byexploiting bit-level parallelism, they can significantly accelerate queries.However, they can use much memory, and thus we might prefer compressed bitmapindexes. Following Oracle’s lead, bitmaps are often compressed using run-len…

arXiv.orgSamy Chambi

Consistently faster and smaller compressed bitmaps with Roaring

Compressed bitmap indexes are used in databases and search engines. Manybitmap compression techniques have been proposed, almost all relying primarilyon run-length encoding (RLE). However, on unsorted data, we can get superiorperformance with a hybrid compression technique that uses both uncompre…

arXiv.orgDaniel Lemire

Roaring Bitmaps: Implementation of an Optimized Software Library

Compressed bitmap indexes are used in systems such as Git or Oracle toaccelerate queries. They represent sets and often support operations such asunions, intersections, differences, and symmetric differences. Severalimportant systems such as Elasticsearch, Apache Spark, Netflix’s Atlas,LinkedIn’…

arXiv.orgDaniel Lemire

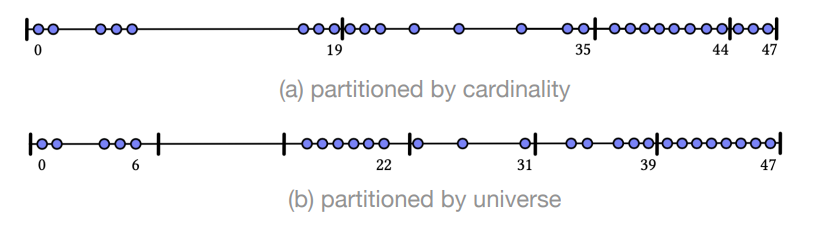
Slicing [Pibiri19]

Sliced Indexes とも
Roaring と同様、 Universe によるパーティショニングを行う
- Roaring が 2 階層までの分割だったのに対して、こちらは最大 3 階層

On Slicing Sorted Integer Sequences

Representing sorted integer sequences in small space is a central problem forlarge-scale retrieval systems such as Web search engines. Efficient queryresolution, e.g., intersection or random access, is achieved by carefullypartitioning the sequences. In this work we describe and compare two diffe…

arXiv.orgGiulio Ermanno Pibiri

実装

Binary Interpolative

BIC [Moffat&Stuiver96, Moffat&Stuiver00]

Binary Interpolative coding (BIC)
2分木を使った再帰的なアルゴリズム
- 中央の要素から深さ優先順にエンコードしていく
S[i, j] の範囲を BIC でエンコードするとき、中央の要素の位置を m とすると、中央の要素は S[m] - low - m + i でエンコードされる
- low はその範囲の最小値 (= S[i])
- S[m] - low は最小値からの相対量
- そこからさらに中央の要素の相対位置を引く
下の例では、 [7, 2, 0, 0, 18, 5, 3, 16, 1, 7] となる
整数列が密なとき、非常にコンパクト
一方で、再帰的なため、デコードは遅め

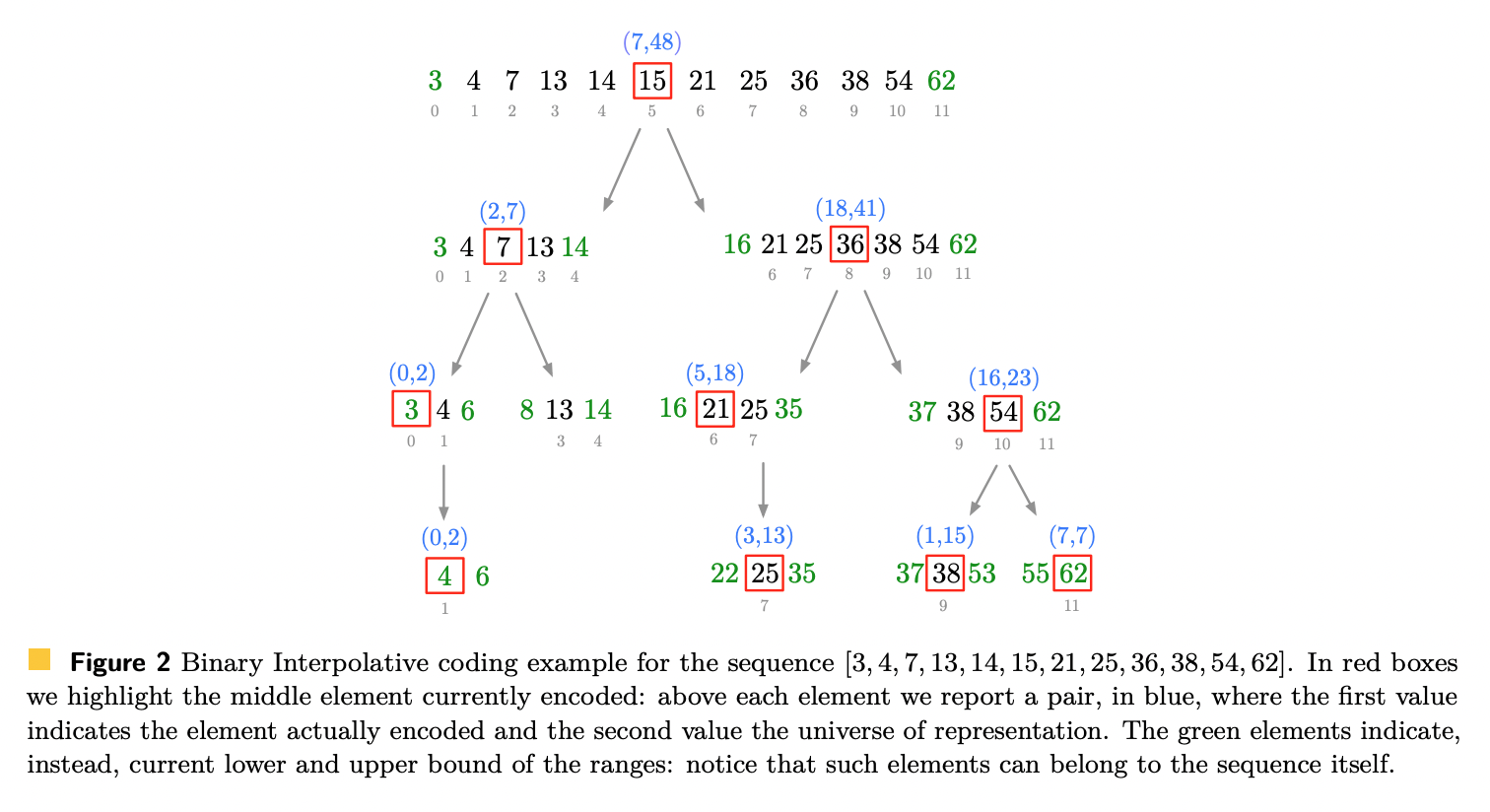
Giulio Ermanno Pibiri and Rossano Venturini. 2020. Inverted Index Compression. Figure 2

Directly-Addressable

ランダムアクセスが可能

DAC [Brisaboa+13]

Directly-addressable code (DAC)
すべての整数を b ビットずつに分割
すべての整数の最初の b ビットをストリーム C1 に入れる、（あれば）次の b ビットを C2 に入れる…と繰り返す
- 1 ビットの制御ビットも入れる（続きがあれば 1、なければ 0）

Nieves R Brisaboa, Susana Ladra, and Gonzalo Navarro. 2013. DACs: Bringing direct access to variable-length codes. Fig. 1

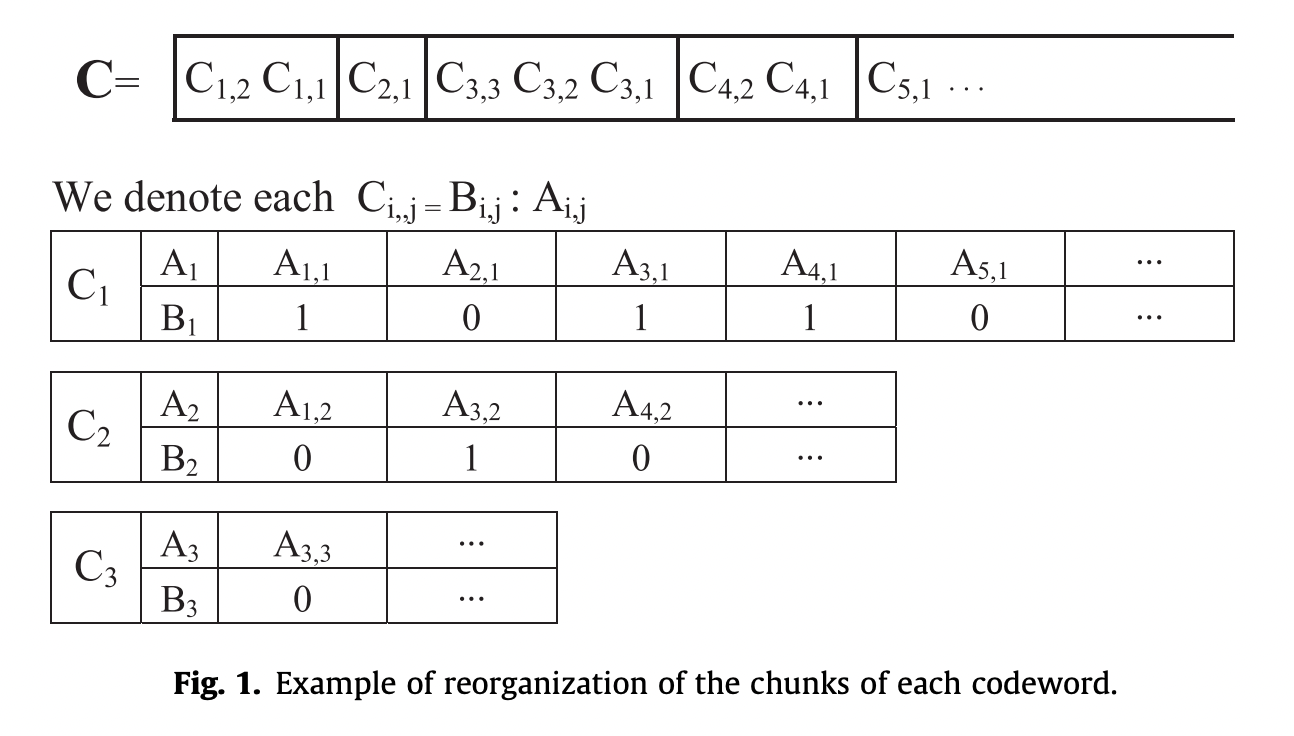
制御ビットの配列 B1, B2, … に対して Rank1 することで、もとの整数配列を全部デコードせずにランダムアクセスが可能
下記の例（記法が論文と少し違うので注意）で L[5] にアクセスしたいとき、
- B1[5] が 1 なので、次のチャンク (C2) にアクセスする必要がある
- C2 のインデックスは Rank1(B1, 5) = 2
- B2[2] は 0 なので、これで終わり
- C1[5] = 101 と C2[2] = 001 を連結して 001.101 (=13) を得る

A Crash Course on Data Compression. 3. List Compressors p.45

実装

https://lbd.udc.es/research/DACS/

Dictionary-based

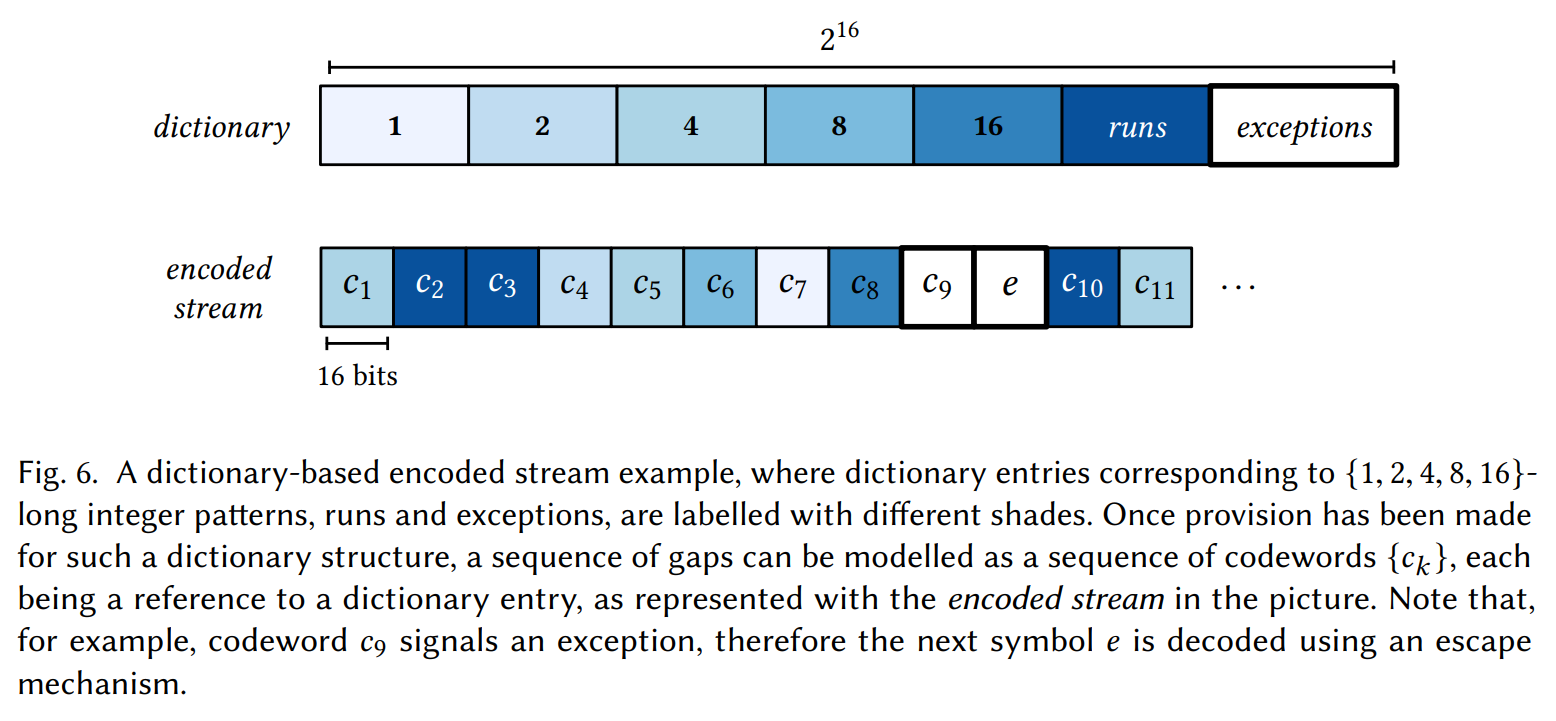
DINT [Pibiri+19]

辞書を使ってポスティングリストの圧縮率を高めた
圧縮率と速度を両立

Giulio Ermanno Pibiri, Matthias Petri, and Alistair Moffat. 2019. Fast Dictionary-Based Compression for Inverted Indexes. Fig. 6

Bitmap Compression

整数値をビットマップで表現する
- 整数 i を表現するとき、ビット配列の i 番目の位置にビットを立てる
- 0100100001 なら 2, 5, 10
このビットマップを圧縮する技法が bitmap compression

整数列圧縮の手法（PforDelta など）と比較して Intersection (AND) は速い
Union (OR) やデコードは整数列圧縮のほうが速い
Roaring はビットマップ圧縮と整数列圧縮のハイブリッド
- 他の bitmap compression の手法と違って RLE (run length encoding) を使っていない
- 全体的に他の bitmap compression の手法より Roaring のほうが良い

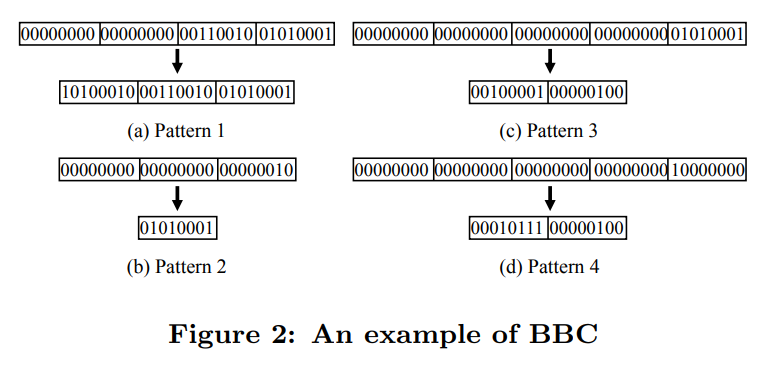
An Experimental Study of Bitmap Compression vs. Inverted List Compression from Takeshi Yamamuro

BBC [Antoshenkov95]

Byte-aligned Bitmap Code
ビットマップを 1 byte (8-bit) ずつに分割
これらの byte を fill byte と literal byte に分類
- fill byte: すべてのビットが同じ byte
- literal byte: それ以外
fill byte と literal byte の並びのパターンごとに圧縮

WAH [Kesheng+01]

Word-Alighned Hybrid
ビットマップを 31-bit ずつの group に分割
これらを fill group と literal group に分類
- fill group: すべてのビットが同じ
- literal group: それ以外
先頭に 1 bit の判定フラグを足す
- 1 なら fill group
fill group は RLE でエンコード
- 2 bit 目に 1-fill group かどうかのフラグをもつ
- 残りの 30 bits に長さをエンコード
literal group はそのまま
Intersection (AND) や Union (OR) はデコードせずに計算可能

EWAH [Lemire+10]

Enhanced Word-Alighned Hybrid
WAH の改良
- literal group が多い場合に WAH は容量効率が悪い
ビットマップを 32-bit の group に分割
p 個（p ≤ 65535）の fill groups と q 個（q ≤ 32767）の literal group をひとかたまりとする
先頭に 32-bit の marker を置く
- 最初の 1 bit: 1-fill group かどうかのフラグ
- 次の 16 bits: fill groups の数 p をエンコード
- 最後の 15 bits: literal groups の数 q をエンコード

Sorting improves word-aligned bitmap indexes

Bitmap indexes must be compressed to reduce input/output costs and minimizeCPU usage. To accelerate logical operations (AND, OR, XOR) over bitmaps, we usetechniques based on run-length encoding (RLE), such as Word-Aligned Hybrid(WAH) compression. These techniques are sensitive to the order of the…

arXiv.orgDaniel Lemire

CONCISE [Colantonio&Pietro10]

Compressed N Composable Integer Set
WAH の改良
- fill group と 1 ビットだけ異なる値をもつ literal group （mixed fill group と呼ぶ）に着目
- そのビットを odd bit と呼び、その位置をエンコードすることで容量を削減する
ビットマップを 31-bit ずつの group に分割（WAHと同じ）
先頭の 1 bit を literal group かどうかの判定フラグにする
- literal group の場合、残りの 31 bits に literal group をそのまま保存
連続する fill group の並びは、以下のように RLE で表現
- EWAH の marker のように fill group の run を 32-bit で表現
- 1 bit 目は 0（literal group と区別するため）
- 2 bit 目に 1-fill group かどうかのフラグをもつ（WAHと同じ）
- 次の 5 bits で odd bit の位置をエンコード
  - odd bit がない場合は 00000
- 残りの 25 bits で fill groups の数 - 1 を保存

CONCISE: Compressed ‘n’ Composable Integer Set

Bit arrays, or bitmaps, are used to significantly speed up set operations inseveral areas, such as data warehousing, information retrieval, and datamining, to cite a few. However, bitmaps usually use a large storage space, thusrequiring compression. Nevertheless, there is a space-time tradeoff am…

arXiv.orgAlessandro Colantonio

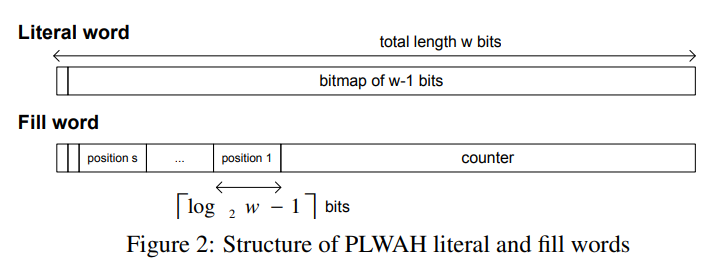
PLWAH [Deliège&Pedersen10]

Position List WAH
CONCISE に似ているが、mixed fill group の表現が異なる

François Deliège and Torben Bach Pedersen. 2010. Position list word aligned hybrid: optimizing space and performance for compressed bitmaps. Figure 1

https://openproceedings.org/2010/conf/edbt/DeliegeP10.pdf

VALWAH [Guzun+14]

Variable-Aligned WAH
WAH は 30 bits の RLE で fill groups の並びを表現していたが、実際には連続する fill groups は少ない
32-bit に複数のセグメントをエンコード
- 可変のセグメント長
容量のオーバーヘッドとクエリの速度のトレードオフを調整するパラメータ lambda をもつ
セグメント長を可変にすることで容量は小さくなるが、アラインメントの問題でクエリは遅い

SBH [Kim+16]

Super Byte-Aligned Hybrid
容量効率を上げるために word-aligned ではなく byte-aligned にした
ビットマップを 7-bit のグループに分割
連続する fill groups の数 k （k ≤ 4093）をエンコード
- k ≤ 63 のとき
  - 1 bit 目は 0
  - 2 bit 目に 1-fill group かどうかのフラグをもつ
  - 残りの 6 bits で k をエンコード
- 63 < k ≤ 4093 のとき、2バイトで fill groups を表現
  - 1 byte 目
    - 1 bit 目は 0
    - 2 bit 目に 1-fill group かどうかのフラグをもつ
    - 残りの 6 bits で k の下位 6 bits をエンコード
  - 2 byte 目
    - 最初の 2 bits は 1 byte 目と同じ
    - 残りの 6 bits で k の上位 6 bits をエンコード

https://dbs.snu.ac.kr/papers/sbh16.pdf

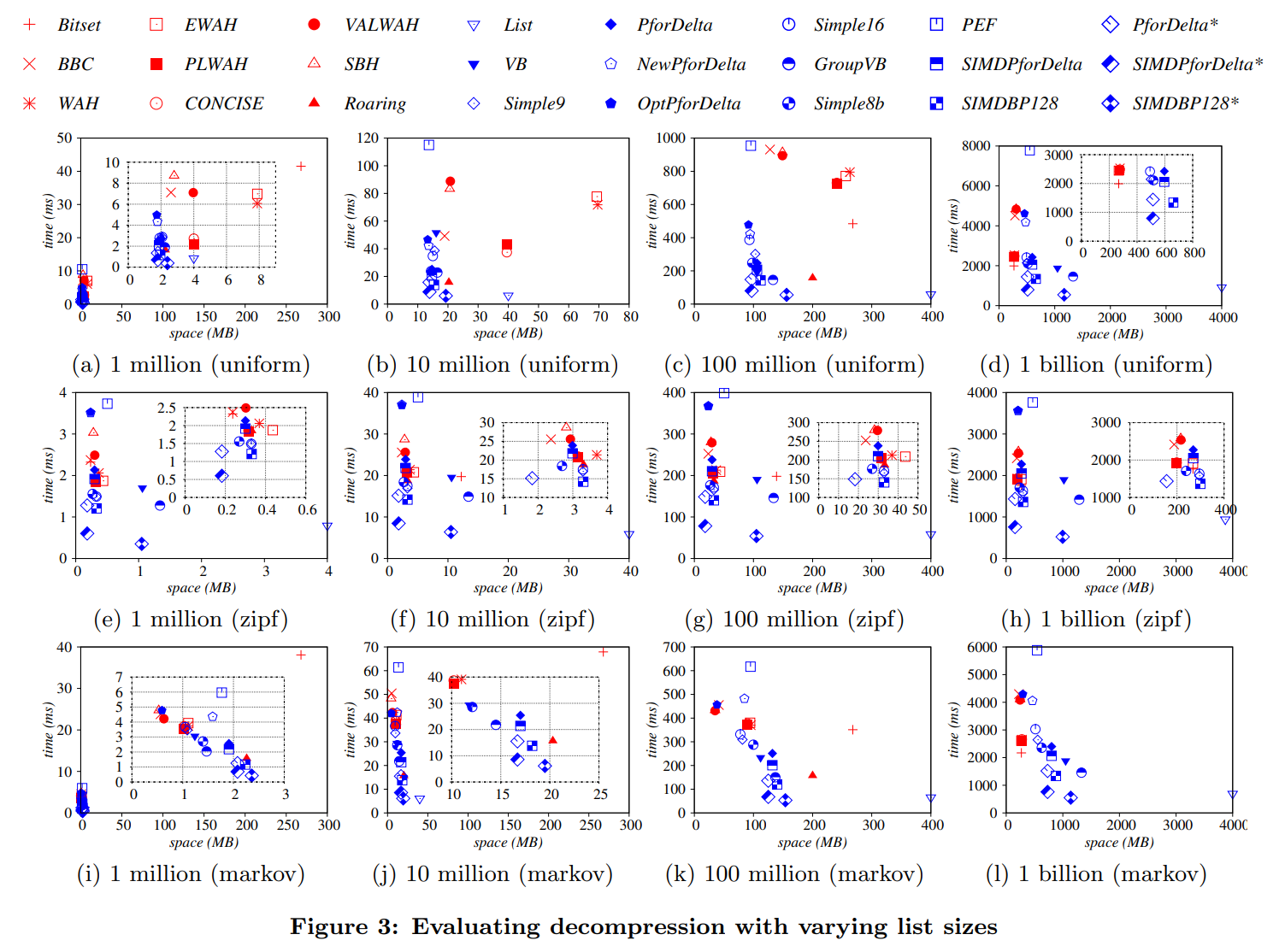
実装とベンチマーク

2i_bench

IcBench

JavaFastPFOR

整数（列）圧縮アルゴリズムとそのベンチマークの Java 実装。以下の実装が含まれる。

BinaryPacking
XorBinaryPacking
DeltaZigzagBinaryPacking
FastPFor
Group Simple9
NewPFD, NewPDFS9, NewPFDS16
OptPFD, OptPFDS9, OptPFDS16
Simple16
Simple9
VByte

現時点 (2022-10-23) では動作させるために Java 19 の実行環境が必要。

ビルドとベンチマークの実行には Maven が使用できる。

mvn compile

mvn exec:java

参考文献

Vo Ngoc Anh and Alistair Moffat. 2005. Inverted Index Compression Using Word-Aligned Binary Codes. Inf. Retr. 8, 1 (January 2005), 151–166. https://doi.org/10.1023/B:INRT.0000048490.99518.5c
Vo Ngoc Anh and Alistair Moffat. 2010. Index compression using 64-bit words. Softw. Pract. Exper. 40, 2 (February 2010), 131–147.
G. Antoshenkov. 1995. Byte-aligned bitmap compression. In Proceedings of the Conference on Data Compression (DCC '95). IEEE Computer Society, USA, 476.
Nieves R Brisaboa, Susana Ladra, and Gonzalo Navarro. 2013. DACs: Bringing direct access to variable-length codes. Information Processing & Management 49, 1 (2013), 392–404.
Stefan Büttcher, Charles Clarke, and Gordon V. Cormack. 2010. Information Retrieval: Implementing and Evaluating Search Engines. The MIT Press.
Samy Chambi, Daniel Lemire, Owen Kaser, and Robert Godin. 2016. Better bitmap performance with Roaring bitmaps. Softw. Pract. Exper. 46, 5 (May 2016), 709–719. https://doi.org/10.1002/spe.2325
Alessandro Colantonio and Roberto Di Pietro. 2010. Concise: Compressed 'n' Composable Integer Set. Inf. Process. Lett. 110, 16 (July, 2010), 644–650. https://doi.org/10.1016/j.ipl.2010.05.018
Jeffrey Dean. 2009. Challenges in building large-scale information retrieval systems: invited talk. In Proceedings of the Second ACM International Conference on Web Search and Data Mining (WSDM '09). Association for Computing Machinery, New York, NY, USA, 1. https://doi.org/10.1145/1498759.1498761
François Deliège and Torben Bach Pedersen. 2010. Position list word aligned hybrid: optimizing space and performance for compressed bitmaps. In Proceedings of the 13th International Conference on Extending Database Technology (EDBT '10). Association for Computing Machinery, New York, NY, USA, 228–239. https://doi.org/10.1145/1739041.1739071
Peter Elias. 1974. Efficient Storage and Retrieval by Content and Address of Static Files. J. ACM 21, 2 (April 1974), 246–260. https://doi.org/10.1145/321812.321820
G. Guzun, G. Canahuate, D. Chiu, and J. Sawin. A tunable compression framework for bitmap indices. In ICDE, pages 484–495, 2014.
Robert Mario Fano. 1971. On the number of bits required to implement an associative memory. Memorandum 61, Computer Structures Group, MIT (1971).
A. S. Kesheng Wu, Ekow J. Otoo and H. Nordberg. Notes on design and implementation of compressed bit vectors, 2001.
S. Kim, J. Lee, S. R. Satti, and B. Moon. Sbh: Super byte-aligned hybrid bitmap compression. IS, 62:155--168, 2016.
Daniel Lemire, Owen Kaser, and Kamel Aouiche. 2010. Sorting improves word-aligned bitmap indexes. Data Knowl. Eng. 69, 1 (January, 2010), 3–28. https://doi.org/10.1016/j.datak.2009.08.006
D. Lemire and L. Boytsov. 2015. Decoding billions of integers per second through vectorization. Softw. Pract. Exper. 45, 1 (January 2015), 1–29. https://doi.org/10.1002/spe.2203
Daniel Lemire, Gregory Ssi-Yan-Kai, and Owen Kaser. 2016. Consistently faster and smaller compressed bitmaps with Roaring. Softw. Pract. Exper. 46, 11 (November 2016), 1547–1569. https://doi.org/10.1002/spe.2402
Daniel Lemire, Owen Kaser, Nathan Kurz, Luca Deri, Chris O’Hara, François Saint-Jacques, and Gregory Ssi-Yan-Kai. 2018. Roaring bitmaps: Implementation of an optimized software library. Software: Practice and Experience 48, 4 (2018), 867–895.
Daniel Lemire, Nathan Kurz, and Christoph Rupp. 2018. Stream VByte: Faster byte-oriented integer compression. Inf. Process. Lett. 130, (February 2018), 1–6. https://doi.org/10.1016/j.ipl.2017.09.011
Christopher D. Manning, Prabhakar Raghavan, and Hinrich Schütze. 2008. Introduction to Information Retrieval. Cambridge University Press, USA.
Alistair Moffat and Lang Stuiver. 1996. Exploiting clustering in inverted file compression. In Proceedings of the Data Compression Conference (DCC’96). 82--91.
Alistair Moffat and Lang Stuiver. 2000. Binary Interpolative Coding for Effective Index Compression. Inf. Retr. 3, 1 (July 2000), 25–47. https://doi.org/10.1023/A:1013002601898
Giuseppe Ottaviano and Rossano Venturini. 2014. Partitioned Elias-Fano indexes. In Proceedings of the 37th international ACM SIGIR conference on Research & development in information retrieval (SIGIR '14). Association for Computing Machinery, New York, NY, USA, 273–282. https://doi.org/10.1145/2600428.2609615
Giulio Ermanno Pibiri, Matthias Petri, and Alistair Moffat. 2019. Fast Dictionary-Based Compression for Inverted Indexes. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining (WSDM '19). Association for Computing Machinery, New York, NY, USA, 6–14. https://doi.org/10.1145/3289600.3290962
Giulio Ermanno Pibiri. 2019. On Slicing Sorted Integer Sequences. CoRR abs/1907.01032 (2019). http://arxiv.org/abs/1907.01032
Giulio Ermanno Pibiri and Rossano Venturini. 2020. On Optimally Partitioning Variable-Byte Codes. IEEE Trans. on Knowl. and Data Eng. 32, 9 (Sept. 2020), 1812–1823. https://doi.org/10.1109/TKDE.2019.2911288
Giulio Ermanno Pibiri and Rossano Venturini. 2020. Techniques for Inverted Index Compression. ACM Comput. Surv. 53, 6, Article 125 (November 2021), 36 pages. https://doi.org/10.1145/3415148
Jeff Plaisance, Nathan Kurz, and Daniel Lemire. 2015. Vectorized VByte Decoding. In International Symposium on Web Algorithms.
Alexander A. Stepanov, Anil R. Gangolli, Daniel E. Rose, Ryan J. Ernst, and Paramjit S. Oberoi. 2011. SIMD-based decoding of posting lists. In Proceedings of the 20th ACM international conference on Information and knowledge management (CIKM '11). Association for Computing Machinery, New York, NY, USA, 317–326. https://doi.org/10.1145/2063576.2063627
Larry H Thiel and HS Heaps. 1972. Program design for retrospective searches on large data bases. Information Storage and Retrieval 8, 1 (1972), 1–20.
Andrew Trotman. 2014. Compression, SIMD, and Postings Lists. In Proceedings of the 2014 Australasian Document Computing Symposium (ADCS '14). Association for Computing Machinery, New York, NY, USA, 50–57. https://doi.org/10.1145/2682862.2682870
Jianguo Wang, Chunbin Lin, Yannis Papakonstantinou, and Steven Swanson. 2017. An Experimental Study of Bitmap Compression vs. Inverted List Compression. In Proceedings of the 2017 ACM International Conference on Management of Data (SIGMOD '17). Association for Computing Machinery, New York, NY, USA, 993–1008. https://doi.org/10.1145/3035918.3064007
Hao Yan, Shuai Ding, and Torsten Suel. 2009. Inverted index compression and query processing with optimized document ordering. In Proceedings of the 18th international conference on World wide web (WWW '09). Association for Computing Machinery, New York, NY, USA, 401–410. https://doi.org/10.1145/1526709.1526764
Jiangong Zhang, Xiaohui Long, and Torsten Suel. 2008. Performance of compressed inverted list caching in search engines. In Proceedings of the 17th international conference on World Wide Web (WWW '08). Association for Computing Machinery, New York, NY, USA, 387–396. https://doi.org/10.1145/1367497.1367550
Marcin Zukowski, Sandor Heman, Niels Nes, and Peter Boncz. 2006. Super-Scalar RAM-CPU Cache Compression. In Proceedings of the 22nd International Conference on Data Engineering (ICDE '06). IEEE Computer Society, USA, 59. https://doi.org/10.1109/ICDE.2006.150

目次

転置インデックスの基本

転置インデックスのデータ構造と特性

転置インデックスのアクセスパターン

近年のインデックス圧縮技法

Variable-Byte Family

VByte (Variable-Byte) [Thiel&Heaps72]

Varint-GB [Dean09]

Varint-G8IU [Stepanov+11]

Masked-VByte [Plaisance+15]

Stream-VByte [Lemire+18]

Opt-VByte [Pibiri&Venturini20]

Simple Family

Simple9 [Anh&Moffat05]

Simple16 [Zhang+08]

Simple8b [Anh&Moffat10]

QMX [Trotman14]

PFor Family

PForDelta [Zukowski+06]

NewPFD [Yan+09]

Opt-PFor [Yan+09]

Fast-PFor, SIMDPforDelta, SIMDBP128 [Lemire&Boytsov15]

Elias-Fano Family

Elias-Fano [Elias74, Fano71]

PEF [Ottaviano&Venturini14]

Roaring [Chambi+16, Lemire+16, Lemire+18]

Slicing [Pibiri19]

Binary Interpolative

BIC [Moffat&Stuiver96, Moffat&Stuiver00]

Directly-Addressable

DAC [Brisaboa+13]

Dictionary-based

DINT [Pibiri+19]

Bitmap Compression

BBC [Antoshenkov95]

WAH [Kesheng+01]

EWAH [Lemire+10]

CONCISE [Colantonio&Pietro10]

PLWAH [Deliège&Pedersen10]

VALWAH [Guzun+14]

SBH [Kim+16]

実装とベンチマーク

2i_bench

IcBench

JavaFastPFOR

参考文献

Sign up for more like this.