近似最近傍探索における新しいビット量子化手法、RaBitQとBBQ
Elasticsearch 8.16 で Better Binary Quantization (BBQ) という、新しい密ベクトルのフィールドタイプが追加されました。
- Dense vector field type | Elasticsearch Guide | Elastic
- Elasticsearch version 8.16.0 New features | Elasticsearch Guide | Elastic
- Adding new experimental bbq index types by benwtrent · Pull Request #114439 · elastic/elasticsearch · GitHub
Elasticsearch ではベクトルの各次元の int8 や int4 への量子化をサポートしていますが、BBQ ではビットにまで量子化することで、さらなるインデックスサイズの削減と近似近傍探索の高速化を図っています。
この記事では、まず BBQ の元になった RaBitQ[1] というベクトル量子化手法を解説します。そのあと、Elasticsearch における BBQ の実装について説明し、RaBitQ と BBQ の違いについて触れます。
この記事は情報検索・検索技術 Advent Calendar 2024 の 25 日目の記事です。
近似最近傍探索 (ANN)
RaBitQ の前に、その背景となっている近似最近傍探索について簡単に説明します。
ANN の問題設定
あるベクトルが与えられたときに、それから近いベクトルを探すタスクを最近傍探索 (NN query; nearest neighbor query) といいます。近似最近傍探索とは、NN のように exact に近いベクトルを探すのではなく、ある程度の誤差を許容するものです。
D 次元のユークリッド空間を考えます。近似最近傍探索 (ANN query; approximate nearest neighbor query) とは、
- クエリベクトル $q$ に対して
- $N$ 個のデータベクトルの集合から
- $K$ 個の近似最近傍ベクトルを取得 (retrieve) する
という問題設定です。ANN query は単に ANN と呼ばれることもよくあります。そのため、以下では ANN と表記します。
言語モデルとベクトル埋め込み
単語や文、文章など、あらゆるテキストデータは言語モデル (LM; language model) により、ベクトルに変換できます。これをベクトル埋め込み (vector embeddings) と呼びます。自然言語処理 (NLP; natural language processing) では通常、100 から 1000 次元程度のベクトルに変換します。このように高次元のベクトル空間に埋め込まれたベクトルのことを、単に埋め込み (embeddings) と呼ぶこともあります。
近年のLM の急速な発展により、「質のよい」ベクトル埋め込みが簡単に計算できるようになりました。つまり、埋め込まれたベクトル空間上で近いベクトル同士は意味が近いとみなせる、ということです。この性質は情報検索 (information retrieval) などのタスクにおいて重要な意味を果たします。
ANN の重要性
データが1次元であれば、 B-tree などのデータ構造で効率的にインデックス化・検索できますが、多次元になると難しくなります。さらに高次元、たとえば自然言語処理で使用されるような 1000 次元クラスになると、kd-tree のような多次元インデックスも役に立ちません。
そこで一定の誤差が生じることを認め、実際はもっと近いベクトルがあるけれど、だいたい近い (approximate nearest neighbor) ベクトルを返せば OK ということにしましょう、という問題設定が ANN です。
NN query から ANN query に問題を緩和 (relax) することで、高次元のベクトル検索を高速に実行することができます。例えば、FAISS、Annoy、FLANN、ScaNN、NGT、DiskANN といった手法(実装)が有名です。これらの手法は、精度 (recall) をある程度保ちながら高速に ANN の K 個のベクトルを検索することができます。他にも、 ann-benchmarks[2] というリポジトリには、ANN のメジャーな手法とそのベンチマーク結果がまとまっています。
ANN は現在も活発に研究開発され、日進月歩でその精度と速度が向上しています。ANN に興味をもった方は、以下のスライド[3]がよくまとまっているので、参考にするとよいでしょう。
ANN とベクトルの量子化
近似最近傍探索 (ANN) のインデックスには、すべてのデータベクトルを保持する必要があります。各データごとに「次元数 x スカラーのデータサイズ (e.g., float32)」の容量が必要になり、効率的とは言えません。
ベクトルの量子化 (quantization) は、一般には float32 や float64 の配列で表現されるベクトルを、 int8 や int4 などのコンパクトな整数表現等に変換する手法です。ベクトルを量子化することでメモリやディスクの使用量を抑え、また SIMD によって検索処理の高速化を狙います。
量子化に関連する代表的な ANN の高速化手法として、直積量子化 (PQ) と転置ファイル (IVF) がよく知られています。また、量子化とは直接関係はないですが、別の ANN 高速化手段として HNSW というグラフベースのインデックス手法があります。
これらについても以下の資料[3:1]に詳しくまとまっています。
直積量子化 (PQ)
代表的なベクトル量子化手法の一つに、直積量子化 (PQ) があります。
ベクトル量子化 (VQ; vector quantization) は、ベクトルの集合を事前計算した K 個のセントロイドで代表する古典的な手法です。VQ では、ベクトルを最も近いセントロイドの ID で表現します。
直積量子化 (PQ; product quantization)[4] は、ベクトルの次元を M 個に分割して、それらのスライスをそれぞれ VQ する方法です。この M 個の代表ベクトル(の ID)の集合をコードブックと呼びます。PQ では、分割した M 個ごとに近いセントロイドを探し、それら M 個の ID で表現します。
転置ファイル (IVF)
また、直積量子化 (PQ) と組み合わせて検索を効率化するデータ構造として、転置ファイル (IVF) があります。
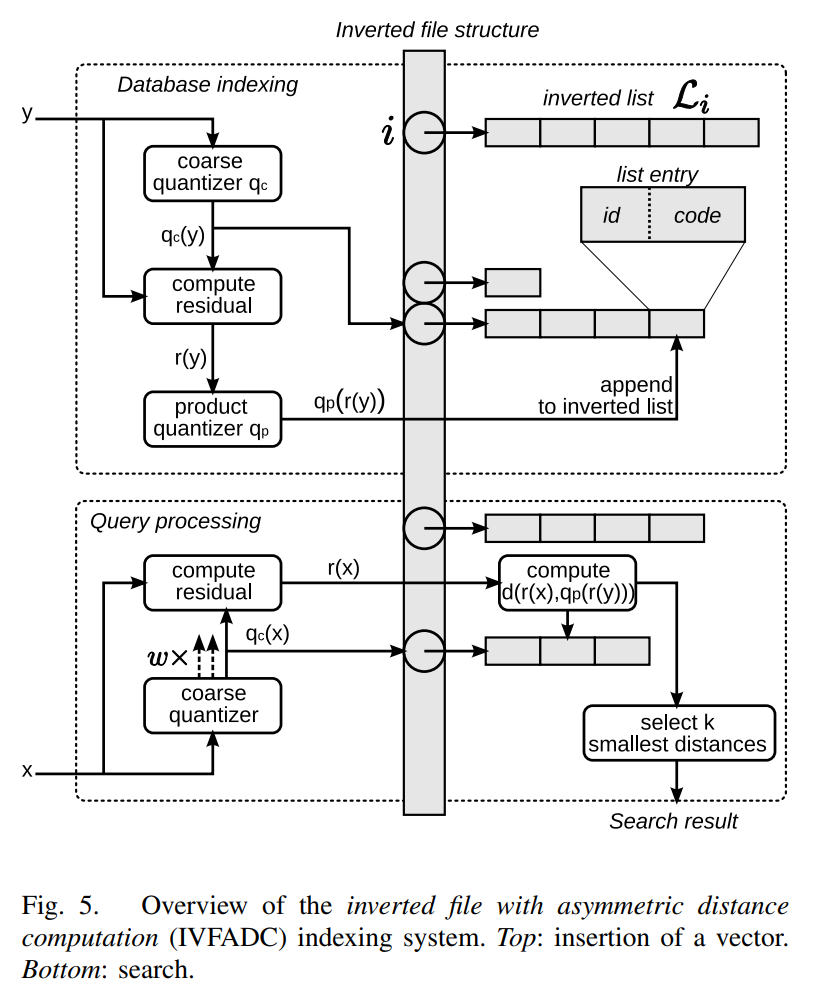
転置ファイル (IVF; inverted file) もしくは IVFADC (Inverted File with Asymmetric Distance Computation)[4:1] とは、転置インデックス的な補助データ構造、およびそれを利用したANN の高速化手法です。IVF ではまず、空間をいくつかに分割し、それぞれの部分空間を代表するセントロイドを用意します。ベクトルが与えられたときに、どの部分空間に入るか(=どのセントロイドが近いか)を計算する粗量子化器 (coarse quantizer) も事前に準備しておきます [5]。
IVF は、以下のように、近いベクトルを代表ベクトル(セントロイド)をキーとした転置リストにまとめます[4:2]。IVF でベクトルを検索するときには、まず量子化したベクトルを計算し、その転置リストを取得します。そのあと得られた転置リストを走査し、最終的な最近傍のベクトルを計算します。
RaBitQ
RaBitQ[1:1] は、Jianyang Gao & Cheng Long によって提案された、新しい ANN インデックスのベクトル量子化手法です。この方法は、ベクトルの各次元を1ビットに量子化することで、インデックスサイズを小さくし、またビット演算や SIMD を活用することで検索処理を高速化しています。RaBitQ の論文では、PQ と比較したときの優位性についても説明されています。
RaBitQ の概要
RaBitQ のアルゴリズムを、インデックスフェイズ(インデックスの構築)とクエリフフェイズ(インデックスからの検索)に分けて説明します。論文[1:2]に合わせて以下のように表記します。
| 表記 | 説明 |
|---|---|
| $\bm{o_r}$ | 元のデータベクトル(正規化・量子化前) |
| $\bm{q_r}$ | 元のクエリベクトル(正規化・量子化前) |
| $\bm{o}$ | 正規化したデータベクトル |
| $\bm{q}$ | 正規化したクエリベクトル |
| $\bm{c}$ | セントロイド(中心ベクトル) |
| $C$ | 量子化ベクトルのコードブック(集合) |
| $C_{rand}$ | コードブック $C$ をランダム化したもの |
| $\overline{\bm{x}}$ | 量子化したデータベクトル(コードブック $C$ の中から選ぶ) |
| $\overline{\bm{o}}$ | 量子化したデータベクトル(コードブック $C_{rand}$ の中から選ぶ)、つまり $\overline{\bm{o}} = P \overline{\bm{x}}$ |
| $\overline{\bm{x}}_b$ | 正規化したデータベクトル $\bm{o}$ を量子化し、ビット表現にしたもの |
| $\bm{q}\rq$ | クエリベクトルをランダム射影の逆行列 $P^{-1}$ で変換したもの( $\bm{q}\rq = P^{-1} \bm{q}$ ) |
| $\overline{\bm{q}}$ | 変換後のクエリベクトル $\bm{q}\rq$ を量子化したもの |
| $\overline{\bm{q}}_u$ | $\overline{\bm{q}}$ の符号なし整数表現 |
RaBitQ では、データベクトル($\bm{o_r}$ の集合)を以下のように量子化・インデキシングします(インデックスフェイズ)。
- セントロイド $\bm{c}$ を計算し、すべてのデータベクトルを正規化($\bm{o_r}$ を $\bm{o}$ にする)
- ランダムな直交行列 $P$ をサンプリングし、コードブック $C_{rand}$ を構築
- 量子化されたデータベクトル $\overline{\bm{x}}_b$ を計算(コードブックの中から選ぶ)
- 以下を事前計算
- データベクトルとセントロイドとの距離 $\Vert \bm{o}_r - \bm{c} \Vert$
- 量子化されたデータベクトルと正規化したデータベクトルの内積 $\langle \overline{\bm{o}}, \bm{o}\rangle$

構築されたインデックスに対して、検索は以下のアルゴリズムで行います(クエリフェイズ)。
- クエリベクトルを正規化・変換
- 1.のクエリベクトルを量子化
- 各データベクトルに対して以下を計算
- $\frac{\langle \bm{\overline{o}}, \bm{q}\rangle}{\langle \bm{\overline{o}}, \bm{o}\rangle}$ を計算($\langle \bm{o}, \bm{q}\rangle$ の近似値として使用する。後述)
- 元のクエリベクトルとデータベクトルの距離の推定値を計算

それでは、RaBitQ の各ステップを詳しく見ていきましょう。まず、インデックスフェイズでもクエリフェイズでも共通で使用されることになる、ベクトルの正規化とコードブックによる量子化について説明します。
ベクトルの正規化
ベクトル $\bm{x}_1, \cdots, \bm{x}_k$ のセントロイド $\bm{c}$ は以下で計算されます。
\[ \bm{c} = \frac{1}{k} (\bm{x}_1 + \cdots + \bm{x}_k) \]
RaBitQ ではまず、与えられたデータベクトル全体から、セントロイド $\bm{c}$ を事前に計算します。
その後、各データベクトル $\bm{o}_r$ に対して、以下のように正規化されたベクトル $\bm{o}$ を得ます:
\[ \bm{o} := \frac{\bm{o}_r - \bm{c}}{\|\bm{o}_r - \bm{c}\|} \]
この様子を可視化したものが以下です[6]。
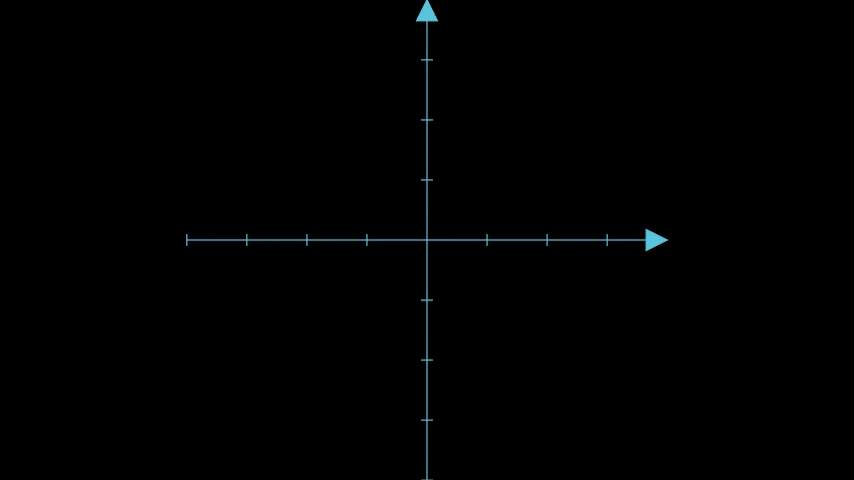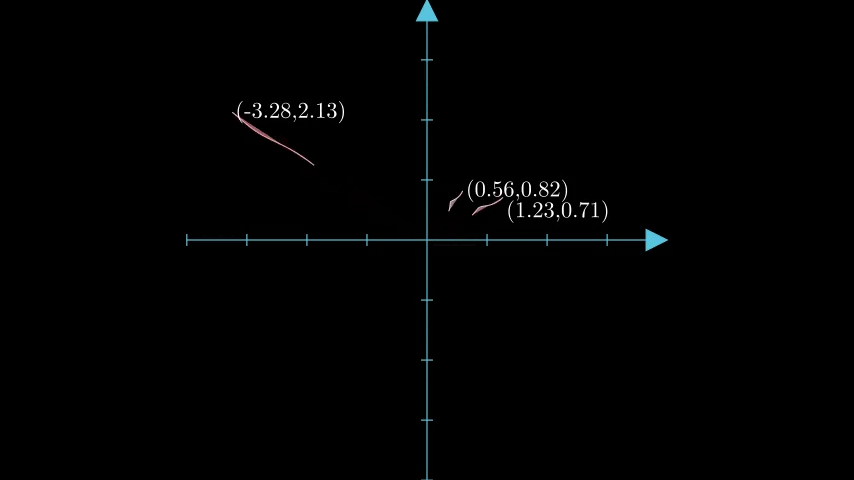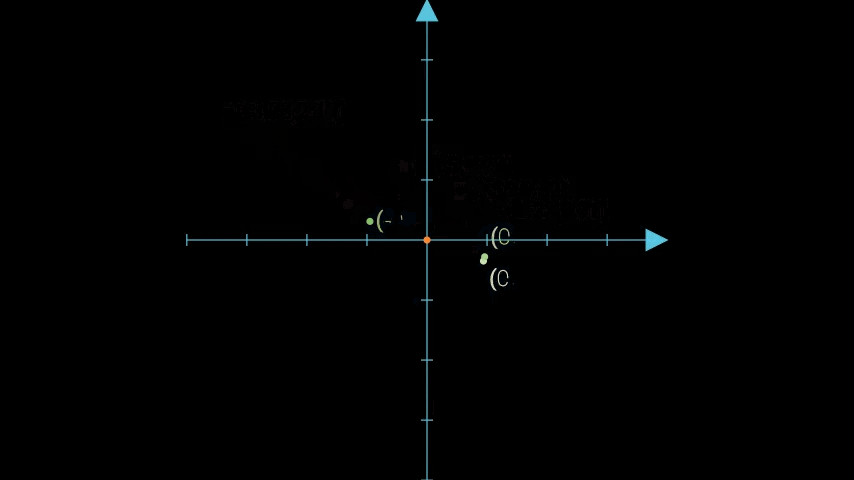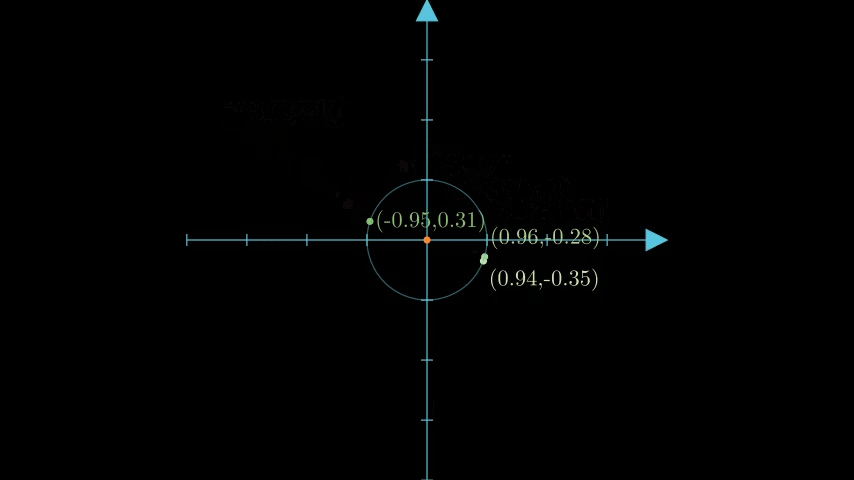
多次元コードブック
次に、正規化したベクトルを量子化することを考えます。代表点(コード)の集合=コードブックを考え、ベクトルをそれに最も近い代表点で表現(近似)することによって量子化できます。
正規化したデータベクトルは、単位球面上に広がって分布することが期待されます[7]。よってコードブックも、単位球面上に一様に分布するように構成します。コードブックの要素(コード)は単位球面上の点なので、単位ベクトルであることに注意します。
ベクトル空間の次元を $D$ としたとき、自然な構成として、コードブックを以下のようにつくることが考えられます。
\[ C := \lbrace +\frac{1}{\sqrt{D}}, -\frac{1}{\sqrt{D}} \rbrace ^D \]
このように構成したコードブックは、具体的には以下のようになります(コードブックは $2^D$ 個の要素をもちます)。
- 1次元: $\lbrace +1, -1 \rbrace$
- 2次元: $\lbrace \lparen +\frac{1}{\sqrt{2}}, +\frac{1}{\sqrt{2}} \rparen, \lparen +\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \rparen, \lparen -\frac{1}{\sqrt{2}}, +\frac{1}{\sqrt{2}} \rparen, \lparen -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \rparen, \rbrace$
- 3次元: $\lbrace \lparen +\frac{1}{\sqrt{3}}, +\frac{1}{\sqrt{3}}, +\frac{1}{\sqrt{3}} \rparen, \dots, \lparen -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}} \rparen \rbrace$
2次元のときの例を考えましょう。2次元の場合、コードブック $\lbrace \lparen +\frac{1}{\sqrt{2}}, +\frac{1}{\sqrt{2}} \rparen, \lparen +\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \rparen, \lparen -\frac{1}{\sqrt{2}}, +\frac{1}{\sqrt{2}} \rparen, \lparen -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \rparen, \rbrace$ の中から、もっとも近い代表点を選ぶことになります。幾何学的に考えると、以下のように、4象限(領域)のそれぞれにコードブックの代表点が対応していると捉えられます[8]。
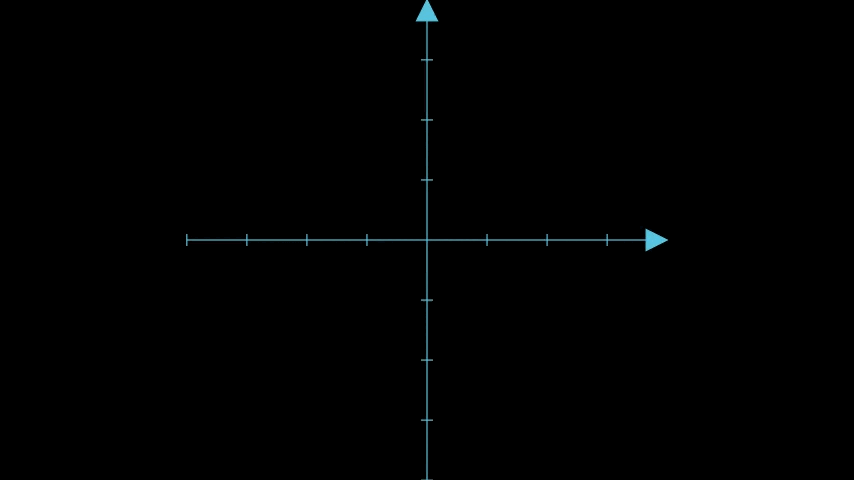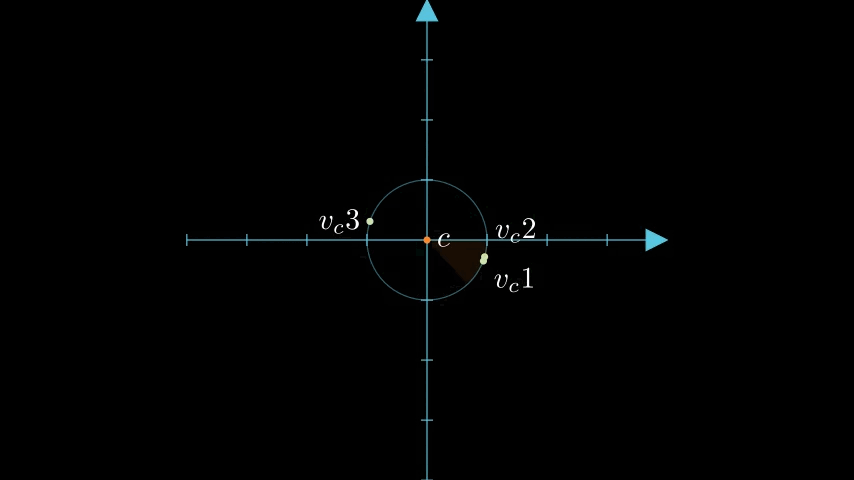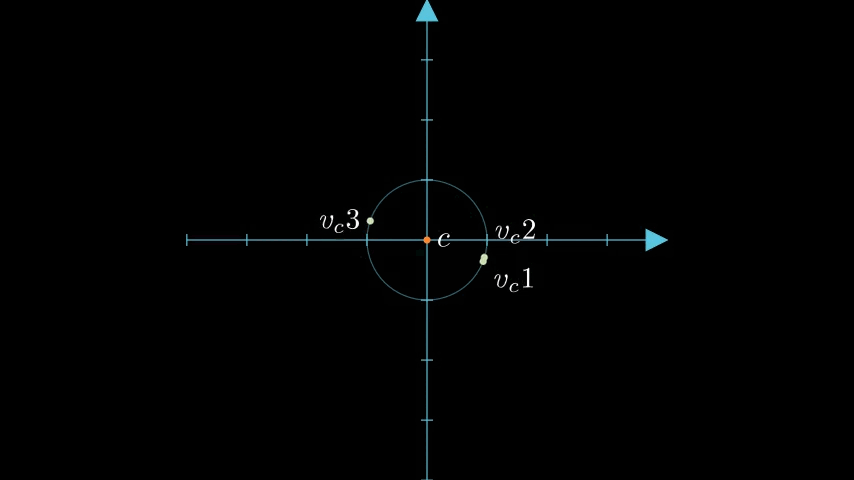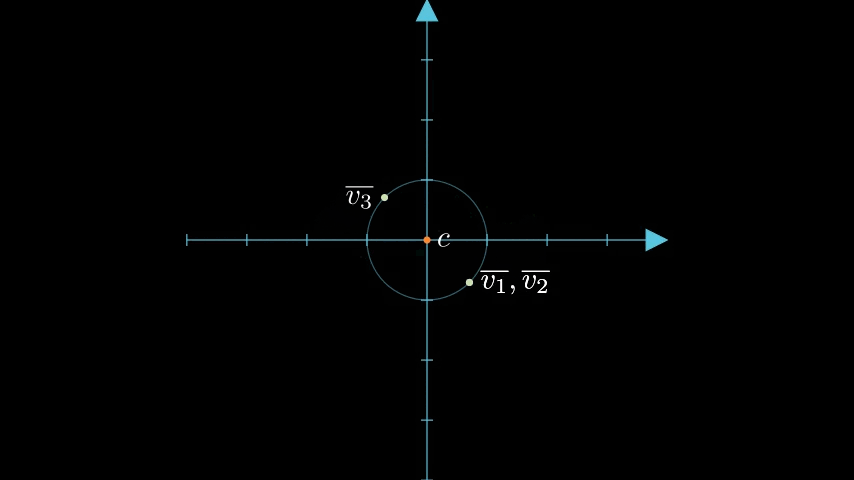
3次元の場合は領域が8個に増えるだけで、同様に各領域の「中心」に代表点が位置することになります。4次元以上になると想像するのが難しくはなりますが同様です。
さて、コードブック $C$ を構成するとき、正規化したデータベクトルが単位球面上に広がって分布することを仮定していました。しかし、恣意的に作成した人工データでもない限り、実際には偏りがあることが想定されます。この偏りを扱うために、RaBitQ では、上記のコードブックのランダム直交射影を考え、それをコードブックとします。
ランダムコードブックの計算
RaBitQ では、コードブック $C$ の各ベクトルをランダムな直交行列 (orthogonal matrix) $P$ で変換したものを最終的なコードブック $C_{rand}$ とします:
\[ C_{rand} := \lbrace P \bm{x} | \bm{x} \in C \rbrace \]
直交行列とは、以下を満たすような正方行列 R のことでした。
\[ R^T R = R R^T = I \]
直交行列の性質として、以下のようなものがあります。
- 直交行列の逆行列は転置行列である: $R^{-1} = R^T$
- 行列 $A$ の逆行列とは $AB = BA = I$ を満たすような行列 B のこと。
- 直交行列の定義から $R^T = R^{-1}$ である。
- 直交行列はノルムを不変に保つ変換である: $\Vert R \bm{u} \Vert = \Vert \bm{u} \Vert$
- R を直交行列、 u を任意のベクトルとしたとき、 $\Vert R\bm{u} \Vert^2 = \langle R\bm{u}, R\bm{u} \rangle = \langle \bm{u}, R^T R\bm{u} \rangle = \langle \bm{u},\bm{u} \rangle = \Vert\bm{u}\Vert^2$。
- よって $\Vert Ru\Vert = \Vert u \Vert$。
- 直交行列による変換は内積を不変に保つ: $\langle R\bm{u}, R\bm{v} \rangle = \langle \bm{u}, \bm{v} \rangle$
- R を直交行列、 u, v を任意のベクトルとしたとき、 $\langle R\bm{u}, R\bm{v} \rangle = \langle \bm{u}, R^T R\bm{v} \rangle = \langle \bm{u},\bm{v} \rangle$
$P$ は直交行列なので、単位ベクトル $\bm{x} \in C$ を変換した $P\bm{x} \in C_{rand}$ もまた単位ベクトルとなります(上記の性質「直交行列はノルムを不変に保つ変換である」より)。つまり、 $C_{rand}$ 上のベクトル(コード)は単位超球面上に分布します。
また、性質「直交行列による変換は内積を不変に保つ」により、この直交行列 $P$ による射影では任意のベクトル間の内積(距離)が保存されます。このランダム直交射影によるベクトルの変換は、1種の Johnson-Lindenstrauss Transformation[9][10] になっています[11]。
このランダム直交行列 $P$ は、各要素を乱数で初期化した行列を QR 分解することで計算できます。RabitQ では以下のように実装されていました[12]。
G = np.random.randn(D, D).astype('float32')
Q, _ = np.linalg.qr(G)
return Q
コードブック $C$ は、 $\lbrace +\frac{1}{\sqrt{D}}, -\frac{1}{\sqrt{D}} \rbrace ^D$ のようにある意味恣意的に構成したものでした。この $P$ のランダム性により、決定性のコードブック $C$ の preference を排除することができます。
$P$ は、あらゆる変換の中からランダムにサンプリングしたものです。つまり、 $P$ により変換されたコードブック $C_{rand}$ は、単位超球面上に一様に(等確率で)分布することになります。
よって、データベクトルに偏りがあったとしても、量子化(コード化)した際、より多様なコードへと分散することが期待できます。詳細は元論文[1:3]の Section 3.1 を参照してください。
データベクトルの量子化
コードブック $C_{rand}$ の計算が終わったので、その中から(正規化した)データベクトル $\bm{o}$ に最も近いものを探し、それをデータベクトルの量子化された表現(コード)とします(インデックスフェイズの3番目のステップに相当)。
ユークリッド距離が最も近いベクトルを探すことは、内積が最も大きくなるベクトルを探すことと同値です。そのベクトルを $\overline{\bm{o}} = P \overline{\bm{x}} \in C_{rand}$ とします。このベクトル $\overline{\bm{o}}$ の $P$ での射影前のベクトルが $\overline{\bm{x}} \in C$ です。これは以下のように書けます。
\[ \begin{align*} \overline{\bm{x}} &= \argmin_{\bm{x} \in C} \Vert \bm{o} - P \bm{x} \Vert^2 \\ &= \argmin_{\bm{x} \in C} (\Vert \bm{o} \Vert^2 + \Vert P \bm{x} \Vert^2 - 2 \langle \bm{o}, P\bm{x} \rangle) \\ &= \argmin_{\bm{x} \in C} (2 - 2 \langle \bm{o}, P \bm{x} \rangle) \\ &= \argmax_{\bm{x} \in C} \langle \bm{o}, P \bm{x} \rangle \end{align*} \]
つまり、 $\langle \bm{o}, P \bm{x} \rangle$ が最大になるような $\bm{x}$ を求めたいわけです。これはさらに以下のように変形できます。
\[ \langle \bm{o}, P \bm{x} \rangle = \langle P^{-1} \bm{o}, P^{-1} P \bm{x} \rangle = \langle P^{-1}\bm{o}, \bm{x} \rangle \]
人工的に構成したコードブックの要素 $\bm{x} \in C$ の各次元の値は $\pm 1 / \sqrt{D}$ でした。ベクトル $P^{-1} \bm{o}$ との内積が最大になるような $\bm{x}$ を決めるには、ただベクトル $P^{-1} \bm{o}$ の各次元の値の符号だけを見ればよいことがわかります[13]。それらの符号さえわかれば、 $\overline{\bm{x}}$ をただ1つに決定することができます。よって、これらの符号の列(長さ $D$ )を $\overline{\bm{x}}_{b} \in \{ 0, 1 \}^D$ と表し、これをインデックスに保存します。
RaBitQ では、データベクトルはこのように量子化します。このように表現することで、各データベクトルは $D$ ビットまで小さくなります。また、 $\overline{\bm{x}} = ( 2 \overline{\bm{x}}_b - \bm{1}_D ) / \sqrt{D}$ によってバイナリ表現 $\overline{\bm{x}}_b$ から量子化したデータベクトル $\overline{\bm{x}}$ を復元します。
データベクトルとクエリベクトルの距離
さて、近似最近傍探索の問題は、クエリベクトル $\bm{o_r}$ とデータベクトル $\bm{q_r}$ のユークリッド距離 $\Vert \bm{o_r} - \bm{q_r} \Vert^2$ が小さいデータベクトルを探すことでした。これはベクトルのノルムの性質 $\Vert \bm{x} - \bm{y}\Vert^2 = \Vert \bm{x} |^2 + \Vert \bm{y} \Vert^2 - 2 \cdot \langle \bm{x}, \bm{y} \rangle$ を使うと、セントロイド $\bm{c}$ を使って以下のように展開できます。
\[ \begin{align} \Vert \bm{o_r} - \bm{q_r} \Vert^2 &= \Vert (\bm{o_r} - \bm{c}) - (\bm{q_r} - \bm{c}) \Vert^2 \\ &= \Vert \bm{o_r} - \bm{c} \Vert^2 + \Vert \bm{q_r} - \bm{c}\Vert^2 - 2 \cdot \langle \bm{o_r} - \bm{c}, \bm{q_r} - \bm{c} \rangle \end{align} \]
ベクトルの正規化のところで述べましたが、正規化したデータベクトルは $\bm{o} := \frac{\bm{o_r} - \bm{c}}{\Vert\bm{o_r} - \bm{c}\Vert}$ でした。また、正規化したクエリベクトルは同様に $\bm{q} := \frac{\bm{q_r} - \bm{c}}{\Vert\bm{q_r} - \bm{c}\Vert}$ と書けます。これらの内積は以下のように書けます。
\[ \begin{align} \langle \bm{o}, \bm{q} \rangle &= \langle \frac{\bm{o_r} - \bm{c}}{\Vert \bm{o_r} - \bm{c} \Vert}, \frac{\bm{q_r} - \bm{c}}{\Vert \bm{q_r} - \bm{c} \Vert} \rangle \\ &= \frac{\langle \bm{o_r} - \bm{c}, \bm{q_r} - \bm{c} \rangle}{\Vert \bm{o_r} - \bm{c} \Vert \cdot \Vert \bm{q_r} - \bm{c} \Vert} \end{align} \]
(3) 式から (4) 式への展開には、内積の性質 $\langle a \bm{x}, \bm{y} \rangle = a \langle \bm{x}, \bm{y} \rangle$ を使用しました。この関係性( (4) 式)を使うと、 (2) 式は以下のように変形できます。
\[ \begin{equation} \Vert \bm{o_r} - \bm{q_r} \Vert^2 = \Vert \bm{o_r} - \bm{c} \Vert^2 + \Vert \bm{q_r} - \bm{c} \Vert^2 - 2 \cdot \Vert \bm{o_r} - \bm{c} \Vert \cdot \Vert \bm{q_r} - \bm{c} \Vert \cdot \langle \bm{o}, \bm{q} \rangle \end{equation} \]
このように、クエリベクトル $\bm{o_r}$ とデータベクトル $\bm{q_r}$ のユークリッド距離 $\Vert \bm{o_r} - \bm{q_r}\Vert^2$ は、いくつかのコンポーネントに分離できます。
(5) 式の最初と最後の項にあらわれる $\Vert \bm{o_r} - \bm{c}\Vert$ は、データベクトルとセントロイドの距離です。セントロイドはインデックス構築時に計算済みのため、これは事前に計算できます。事前計算した $\Vert \bm{o_r} - \bm{c} \Vert$ はインデックスと一緒に保存しておきます(インデックスフェイズの4番目)。また、クエリベクトルとセントロイドの距離 $\Vert \bm{q_r} - \bm{c} \Vert$ は検索時に1回だけ計算すればよいため、問題にはなりません。
では、最後のコンポーネントである内積 $\langle \bm{o}, \bm{q} \rangle$ を RaBitQ がどう計算するかを見ていきます。
データベクトルとクエリベクトルの内積の推定
RabitQ では、内積 $\langle \bm{o}, \bm{q} \rangle$ の推定値として $\frac{\langle \overline{\bm{o}}, \bm{q} \rangle}{\langle \overline{\bm{o}}, \bm{o} \rangle}$ を使用します。
データベクトル $\bm{o}$ とクエリベクトル $\bm{q}$ が共線 (colinear) である、つまり $\bm{o} = \bm{q}$ もしくは $\bm{o} = - \bm{q}$ であるとき、 $\langle \overline{\bm{o}}, \bm{q} \rangle = \langle \overline{\bm{o}}, \bm{o} \rangle \cdot \langle \bm{o}, \bm{q} \rangle$ が成り立ちます(共線であれば任意のベクトルに対して成り立つ)。この場合、内積 $\langle \bm{o}, \bm{q} \rangle$ については簡単に解けて、
\[ \begin{equation} \langle \bm{o}, \bm{q} \rangle = \frac{\langle \overline{\bm{o}}, \bm{q} \rangle}{\langle \overline{\bm{o}}, \bm{o} \rangle} \end{equation} \]
となります。これを推定値として使います。共線でないときにはもちろん誤差が出ますが、この誤差は $O(1 / \sqrt{D})$ 以下( $D$ はデータベクトル・クエリベクトルの次元数)であり、かつ unbiased[14] になることが論文中[1:4]の Section 3.2 で証明されています。
$\langle \overline{\bm{o}}, \bm{o} \rangle$ はデータベクトルだけから事前に計算できるため、これもインデックスに保存しておきます(インデックスフェイズの4番目のステップ)[15]。 $\langle \overline{\bm{o}}, \bm{q} \rangle$ の計算については後述します。
RabitQ のインデックスフェイズ
ここで、RabitQ でのデータベクトルの量子化・インデキシングをまとめておきましょう(再掲)。
- セントロイド $\bm{c}$ を計算し、すべてのデータベクトルを正規化($\bm{o_r}$ を $\bm{o}$ にする)
- ランダムな直交行列 $P$ をサンプリングし、コードブック $C_{rand}$ を構築
- 量子化されたデータベクトル $\overline{\bm{x}}_b$ を計算(コードブックの中から選ぶ)
- 以下を事前計算
- データベクトルとセントロイドとの距離 $\Vert \bm{o}_r - \bm{c} \Vert$
- 量子化されたデータベクトルと正規化したデータベクトルの内積 $\langle \overline{\bm{o}}, \bm{o}\rangle$ (オプション)

インデックスには以下の情報を保存します。
- セントロイド $\bm{c}$
- 量子化されたデータベクトル $\overline{\bm{x}}_b$ (データベクトルごとに $D$ ビット)
- 各データベクトルとセントロイドとの距離 $\Vert \bm{o}_r - \bm{c}\Vert$
- 量子化されたデータベクトルと正規化したデータベクトルの内積 $\langle \overline{\bm{o}}, \bm{o}\rangle$ (オプション)
データベクトルとクエリベクトルの内積の近似計算
さて、データベクトルとクエリベクトルの内積((6) 式)を計算するためには、残る $\langle \overline{\bm{o}}, \bm{q} \rangle$ を計算すればよくなりました。これはランダム射影 $P$ を使うと、以下のように変形できます。
\[ \begin{equation} \langle \overline{\bm{o}}, \bm{q} \rangle = \langle P \overline{\bm{x}}, \bm{q} \rangle = \langle P^{-1} P \overline{\bm{x}}, P^{-1} \bm{q} \rangle = \langle \overline{\bm{x}}, \bm{q}\rq \rangle \end{equation} \]
ここで、 $\overline{\bm{x}}$ は量子化後のデータベクトルです。また、便利のために $\bm{q}\rq = P^{-1} \bm{q}$ とおきました。
クエリベクトルの量子化
もともと (6) 式は近似ですから、 (7) 式も正確な値を計算する必要はなく、一定の誤差を許容した近似値で代用できます。RaBitQ では $\bm{q}\rq$ の代わりに、それを量子化したものを使って計算を効率化しています。ただし 1 ビットではなく、誤差を抑えるために $B_q$ ビットで量子化します(非対称な量子化)。
$\bm{q}\rq$ を量子化したものを $\overline{\bm{q}}$ としましょう。前のセクションで $\langle \overline{\bm{x}}, \bm{q}\rq \rangle$ を計算したいという話をしましたが、 $\langle \overline{\bm{x}}, \overline{\bm{q}} \rangle$ をこの近似として使います。
- $v_l \coloneqq \min_{1 \leq i \leq D} \bm{q}\rq[i]$ ( $\bm{q}\rq$ の最小値)
- $v_r \coloneqq \max_{1 \leq i \leq D} \bm{q}\rq[i]$( $\bm{q}\rq$ の最大値)
- $\Delta \coloneqq (v_r - v_l) / (2^{B_q} - 1)$ (量子化の刻み幅)
- $u_i$ を $[0, 1]$ の一様分布からサンプリングした値
としたとき、RaBitQ では $\overline{\bm{q}}$ のバイナリ表現 $\overline{\bm{q}}_u$ (の $i$ 番目の要素)を以下の式で計算します。
\[ \begin{equation} \overline{\bm{q}}_u [i] \coloneqq \lfloor \frac{\bm{q}\rq[i] - v_l}{\Delta} + u_i \rfloor \end{equation} \]
この計算は直感的には、離散化するときに「左」の離散値にするか「右」の離散値にするかを 1/2 の確率で選んでいることになります。こうすることにより、値の分布に依存せずに unbiased にすることができます[16]。
バイナリ表現 $\overline{\bm{q}}_u$ から $\overline{\bm{q}}$ を復元するには、 $\overline{\bm{q}} = \Delta \cdot \overline{\bm{q}}_u + v_l \cdot \bm{1}_D$ ( $\bm{1}_D$ はすべて 1 が立っているビットベクトル)とすればOKです。
クエリベクトルのビット数 $B_q$ を $\Theta (\log \log D)$ としたとき、高い確率で近似による量子化誤差 $| \langle \overline{\bm{x}}, \bm{q}\rq \rangle - \langle \overline{\bm{x}}, \overline{\bm{q}} \rangle |$ が $O(1/ \sqrt{D})$ に収まることが論文中で証明されています(Theorem 3.3[1:5])。また実験的にも、 $D = 128$ (SIFTデータセット)や $D = 960$ (GISTデータセット)の場合に、 $B_q = 4$ まで増やすと誤差が十分に小さく収束することが示されています(Fig. 6[1:6])。
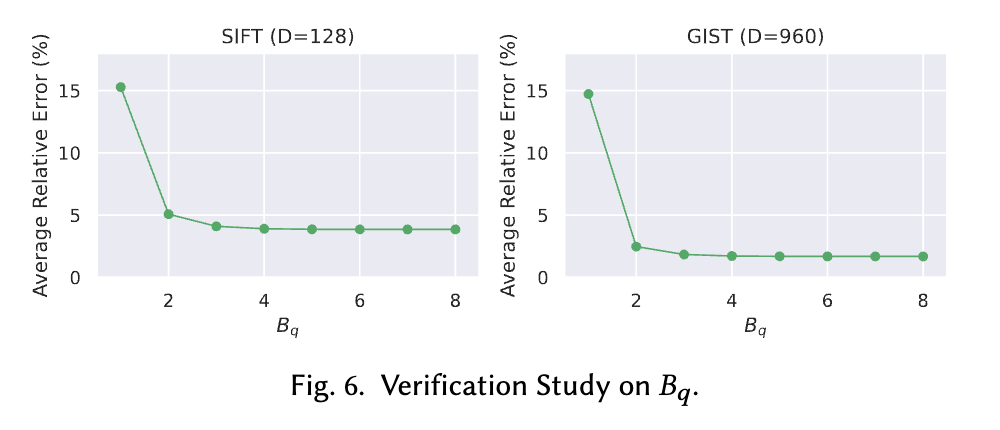
量子化したデータベクトルとクエリベクトルの内積計算
さて、データベクトルのバイナリ表現 $\overline{\bm{x}}_b$ とクエリベクトルのバイナリ表現 $\overline{\bm{q}}_u$ を得たところで、これを使って前述した $\langle \overline{\bm{x}}, \overline{\bm{q}} \rangle$ を計算するのが次の関心事になります。これを効率的に計算するために、ビット演算を利用できる形に変形していきます。
$\overline{\bm{x}} = ( 2 \overline{\bm{x}}_b - \bm{1}_D ) / \sqrt{D}$ 、 $\overline{\bm{q}} = \Delta \cdot \overline{\bm{q}}_u + v_l \cdot \bm{1}_D$ でしたから、 $\langle \overline{\bm{x}}, \overline{\bm{q}} \rangle = \left\langle \frac{2 \overline{\bm{x}}_b - \bm{1}_D}{\sqrt{D}}, \Delta \cdot \overline{\bm{q}}_u + v_l \cdot \bm{1}_D \right\rangle$ です。これはさらに、
\[ \begin{equation} \langle \overline{\bm{x}}, \overline{\bm{q}} \rangle = \frac{2 \Delta}{\sqrt{D}} \langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle + \frac{2 v_l}{\sqrt{D}} \sum_i^D \overline{\bm{x}}_b [i] - \frac{\Delta}{\sqrt{D}} \sum_i^D \overline{\bm{q}}_u [i] - \sqrt{D} \cdot v_l \end{equation} \]
という形に展開できます。この第 2 項に表れる $\sum_i \overline{\bm{x}}_b \lbrack i \rbrack$ は、このビットベクトルの 1 の立っている数であり、インデックスフェイズに事前計算できます。
また、 $D$ は固定値であり、 $\Delta$ や $v_l$ はクエリベクトルの量子化時にすでに計算されています。同様に第3項の $\sum^D \overline{\bm{q}}_{u} [i]$ もクエリ時に一度だけ計算すればよく、計算コストはほとんどかかりません。つまり、第1項の $\langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle$ をどう効率的に計算するかが主な関心になります。
SIMD による内積計算の高速化
ここで、 $D$ 次元のクエリベクトルのバイナリ表現 $\overline{\bm{q}}_u$ を 4 ビット( $B_q = 4$ )として、データベクトルのバイナリ表現 $\overline{\bm{x}}_b$ との内積計算を考えてみましょう。Fig. 2 の左図の点線がクエリの1つの次元です(4 ビット表現)。クエリは $4D$ ビットで表現されることになり、各セルは 0/1 のバイナリの値です。
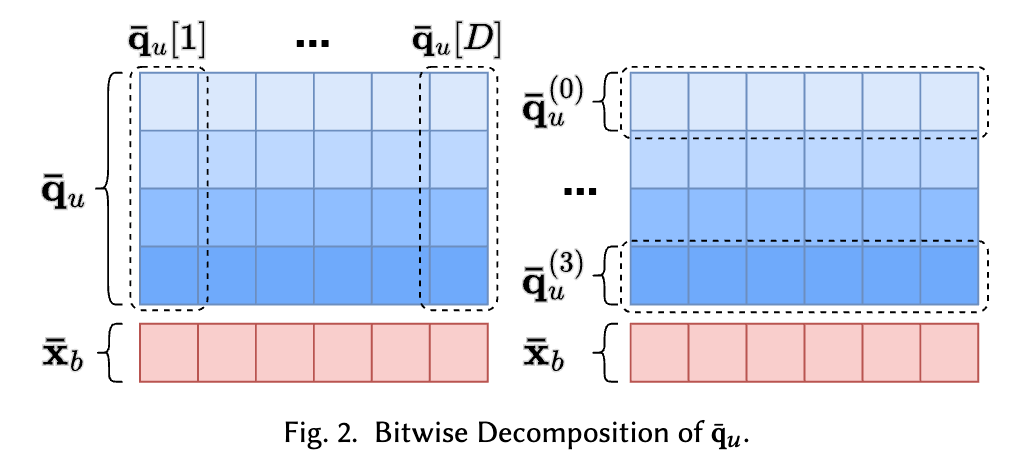
内積の値は1次元ずつ計算できて $\langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle = ( {\overline{\bm{q}}_u}^{(0)} [1] \cdot 2^0 + {\overline{\bm{q}}_u}^{(1)} [1] \cdot 2^1 + {\overline{\bm{q}}_u}^{(2)} [1] \cdot 2^2 + {\overline{\bm{q}}_u}^{(3)} [1] \cdot 2^3 ) + \cdots$ となります。一方、加算は交換できるので、0ビット目から4ビット目までを別々に計算することもできます。つまり、 $\langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle = ( {\overline{\bm{q}}_u}^{(0)} [1] \cdot 2^0 + {\overline{\bm{q}}_u}^{(0)} [2] \cdot 2^0 + {\overline{\bm{q}}_u}^{(0)} [3] \cdot 2^0 + {\overline{\bm{q}}_u}^{(0)} [4] \cdot 2^0 + \cdots ) + \cdots$ で計算することもできます(Fig. 2 右図)。
こうすることで、各ビットベクトル ${\overline{\bm{q}}_u}^{(0)}$ 、 ${\overline{\bm{q}}_u}^{(1)}$ 、 ${\overline{\bm{q}}_u}^{(2)}$ 、 ${\overline{\bm{q}}_u}^{(3)}$ と ${\overline{\bm{x}}_b}$ の論理積(AND)をとったあと、1が立っている数をカウントし、積和演算(それぞれ 1, 2, 4, 8 を掛けて足す)することで内積が求まります。
これは SIMD 演算で効率的に計算することができ、とくにビットを数えるステップは popcount として知られる専用の命令を使用することで高速に計算できます。たとえば SSE や AVX では POPCNT と呼ばれる命令群が用意されています。
論文[1:7]の Section 3.3.2 ではさらに、複数のデータベクトルをバッチで処理することでクエリを高速化する方法についても述べられています。
内積計算の最適化の具体例
この内積計算をもう少し具体的に見てみましょう。以下はクエリベクトルが [8, 15, 10, 7, 4, 0, 9, 9] のときの例です[17]。
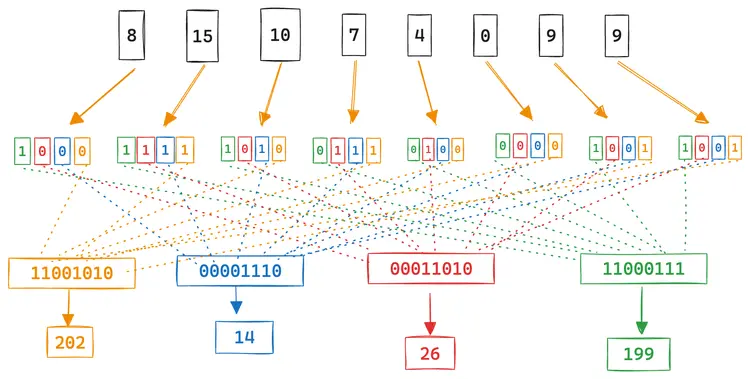
要素はそれぞれ 4 ビットで表現されています。クエリベクトルは 8 次元ごとに分割します(8x4 = 32 ビット単位)。この例では 8 次元ちょうどなのでそのままです。次に、8 個の 4 ビットの各位置のビット(0 ビット目から 4 ビット目まで)を取り出し、4 つの int8 に変換します。
データベクトルは 1 ビット、クエリベクトルは 4 ビットで量子化されるのでした。量子化されたデータベクトルを [0, 1, 1, 0, 0, 0, 0, 0] 、クエリベクトルを [8, 15, 10, 7, 4, 0, 9, 9] として、その内積を計算してみましょう。
普通に計算すると、 0 * 8 + 1 * 15 + 1 * 10 + 0 * 7 + 0 * 4 + 0 * 0 + 0 * 9 + 0 * 9 == 15 + 10 == 25 ですね。この内積計算をビット演算を利用して高速化します。
量子化されたクエリベクトル [8, 15, 10, 7, 4, 0, 9, 9] のバイナリ表現は、先頭から
0b1000(=8)0b1111(=15)0b1010(=10)0b0111(=7)0b0100(=4)0b0000(=0)0b1001(=9)0b1001(=9)
ですね。データベクトルが 1 の次元だけ計算すればよいので、2番目 (0b1111 = 15) と3番目 (0b1010 = 10) を足せば答え (0b1111 + 0b1010 = 25) が求まります。この計算をビット演算風に表現すると (1 + 1) << 3 + (1 + 0) << 2 + (1 + 1) << 1 + (1 + 0) << 0 == 2 * (2**3) + 1 * (2**2) + 2 * (2**1) + 1 * (2**0) == 25 です。
つまり、データベクトル 0, 1, 1, 0, 0, 0, 0, 0] でマスクしたあと(2番目と3番目だけが残る)、各ビット位置ごとにビット数をカウントし、最終的な結果を計算すればよいわけです。これらの計算は、論理積 (AND)、ビットカウント、ビットシフト、そして加算のみで計算できます。
このように、異なるビット数のベクトル同士の内積計算を、簡単なビット演算に帰着させることができます。
RaBitQ のクエリフェイズ
ここまでをおさらいします。インデックスには以下の情報が保存されています:
- セントロイド $\bm{c}$
- 量子化されたデータベクトル $\overline{\bm{x}}_b$ (データベクトルごとに $D$ ビット)
- 各データベクトルとセントロイドとの距離 $\Vert \bm{o}_r - \bm{c}\Vert$
- 量子化されたデータベクトルと正規化したデータベクトルの内積 $\langle \overline{\bm{o}}, \bm{o}\rangle$ (オプション)
計算したいのは生のデータベクトル $\bm{o_r}$ とクエリベクトル $\bm{q_r}$ の距離でした。 (5) 式を思い出してください。
\[ \begin{equation*} \Vert \bm{o_r} - \bm{q_r} \Vert^2 = \Vert \bm{o_r} - \bm{c} \Vert^2 + \Vert \bm{q_r} - \bm{c} \Vert^2 - 2 \cdot \Vert \bm{o_r} - \bm{c} \Vert \cdot \Vert \bm{q_r} - \bm{c} \Vert \cdot \langle \bm{o}, \bm{q} \rangle \end{equation*} \]
$\Vert \bm{o}_r - \bm{c}\Vert$ はインデックスに保存されていますし、 $\bm{c}$ も保存されているため $\Vert \bm{q_r} - \bm{c}\Vert$ もクエリ時に直ちに計算できます。残る $\langle \bm{o}, \bm{q} \rangle$ は (6) 式で近似するのでした:
\[ \begin{equation*} \langle \bm{o}, \bm{q} \rangle = \frac{\langle \overline{\bm{o}}, \bm{q} \rangle}{\langle \overline{\bm{o}}, \bm{o} \rangle} \end{equation*} \]
内積 $\langle \overline{\bm{o}}, \bm{o}\rangle$ はインデックスに保存されているためそれを使います[18]。内積 $\langle \overline{\bm{o}}, \bm{q}\rangle$ は $\langle \overline{\bm{x}}, \overline{\bm{q}} \rangle$ で近似するのでした。(9) 式を思い出します。
\[ \begin{equation*} \langle \overline{\bm{x}}, \overline{\bm{q}} \rangle = \frac{2 \Delta}{\sqrt{D}} \langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle + \frac{2 v_l}{\sqrt{D}} \sum_i^D \overline{\bm{x}}_b [i] - \frac{\Delta}{\sqrt{D}} \sum_i^D \overline{\bm{q}}_u [i] - \sqrt{D} \cdot v_l \end{equation*} \]
前述した通り、第2項以降は素直に計算してもそれほどコストはかかりません。第1項の内積 $\langle \overline{\bm{x}}_b, \overline{\bm{q}}_u \rangle$ は、データベクトルごとにビット演算と SIMD で計算します。
以上をまとめると、RaBitQ のクエリフェイズは以下の通りです(再掲)。
- クエリベクトルを正規化・変換
- 1.のクエリベクトルを量子化
- 各データベクトルに対して以下を計算
- $\frac{\langle \bm{\overline{o}}, \bm{q}\rangle}{\langle \bm{\overline{o}}, \bm{o}\rangle}$ を計算($\langle \bm{o}, \bm{q}\rangle$ の近似値として使用する)
- 元のクエリベクトルとデータベクトルの距離の推定値を計算((5) 式より)

RaBitQ と ANN
クエリフェイズのデータベクトルごとに計算する部分(擬似コードの3行目から5行目)は、前述した IVF といった ANN の手法を併用して高速化できます(Section 4 を参照)。RaBitQ では、バッチでのクエリフェイズの計算が困難という理由で、HNSW のようなグラフベースの手法ではなく、 IVF を使って ANN による高速化を行っています。
RaBitQ では IVF のインデックスからデータベクトルを多めに取得し、リランキングします。RaBitQ では誤差の上限が計算できるため、それを利用してリランク対象のデータベクトルの数を調整します。
RaBitQ の拡張
RaBitQ はデータベクトルを 1 ビットで表現する手法でした。これを複数ビットに拡張することでさらに誤差を下げる手法 Extended RaBitQ[19] が提案されています。この手法については以下のブログポストが参考になるでしょう。
Extended RaBitQ: an Optimized Scalar Quantization Method
BBQ
BBQ (Better Binary Quantization) は、Elastic で開発されたビット量子化手法です。RaBitQ から着想を得て開発されたとのことです。
- RaBitQ binary quantization 101 - Elasticsearch Labs
- Better Binary Quantization (BBQ) in Lucene and Elasticsearch - Elasticsearch Labs
- Smokin' fast BBQ with hardware accelerated SIMD instructions - Elasticsearch Labs
- Better Binary Quantization vs. Product Quantization - Elasticsearch Labs
Elasticsearch での利用方法
Elasticsearch 8.16 以降、BBQ が dense_vector フィールドとして使用できるように Elasticsearch に組み込まれています。 dense_vector フィールドの mapping 定義で、 index_options.type に以下のいずれかを設定することができます:
bbq_hnsw(グラフベースの HNSW で ANN のデータベクトルを取得)bbq_flat(ブルートフォースで kNN のデータベクトルを取得)
{
"mappings": {
"properties": {
"my_vector": {
"type": "dense_vector",
"dims": 64,
"index": true,
"index_options": {
"type": "bbq_hnsw"
}
}
}
}
}
詳細は公式ドキュメントを参照してください。
BBQ によるデータベクトルの量子化
BBQ では RaBitQ と同様に、データベクトルの各次元を1ビットに量子化します。
データベクトルのセントロイドは事前に計算しておく点も同様です。セントロイドの計算は、データベクトルが入ってくるたびにインメモリでインクリメンタルに実行できるので、インデックス構築時にはすでに計算が終わっています。
データベクトルは以下のように 8 次元単位で量子化します[17:1]。
- データベクトルからセントロイドを引く(正規化)
- 1のベクトルの各次元の値が 0 より大きければ
1、そうでなければ0に量子化 - corrections を事前計算
- データベクトルからセントロイドの距離(1 で計算済み)
- 元のデータベクトルと、量子化後のベクトルの内積(どのくらい離れていたか)
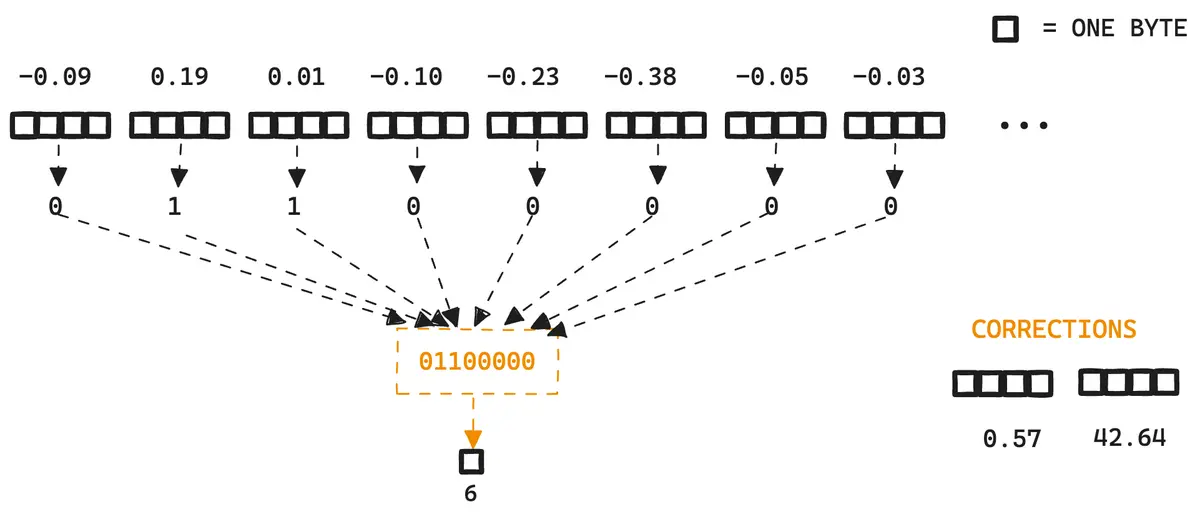
BBQ での距離推定
corrections は検索時に量子化によって失われた情報を「復元」し、クエリベクトルとデータベクトルの距離をより正確に推定するために使います。このあたりは RaBitQ と同様の計算しているようです。さらに詳しい解説は以下のブログを参照してください。
BBQ のバイナリフォーマット
BBQ が Lucene インデックスに保存されるときのバイナリフォーマットは以下のようになっています[17:2]。

量子化されたデータベクトルは 8 次元ずつ pack されます。8次元ごとに量子化されたビットをまとめて byte として保存します。その直後に corrections (長さ 2 から 3 の float の配列)を置く形になっています。
BBQ のインデックス構築の実装
インデックスへの書き込みの実装はこのあたりです:
- https://github.com/elastic/elasticsearch/blob/6c2f6071b20633fafc383212331f79146613011b/server/src/main/java/org/elasticsearch/index/codec/vectors/es816/ES816BinaryQuantizedVectorsWriter.java#L147-L216
- quantizeForIndex https://github.com/elastic/elasticsearch/blob/6c2f6071b20633fafc383212331f79146613011b/server/src/main/java/org/elasticsearch/index/codec/vectors/es816/BinaryQuantizer.java#L245-L300
- generateSubSpace https://github.com/elastic/elasticsearch/blob/6c2f6071b20633fafc383212331f79146613011b/server/src/main/java/org/elasticsearch/index/codec/vectors/es816/BinaryQuantizer.java#L98-L114
距離 (similarity) がユークリッドノルムの場合の流れをまとめてみると、以下のようになります。
- データベクトルとセントロイドの距離を計算
- データベクトルからセントロイドを引く(「正規化」)
- (量子化前後のデータベクトルのノルム(内積)を計算)
- データベクトルを量子化して書き込み(0より大きければ
1) - (3で計算したノルムとデータベクトルからprojection? を計算)
- 上記1と5で計算したものを corrections(2つの float の値)として保存
BBQ のクエリ処理
BBQ では RaBitQ と同様、データベクトルの各次元を 1 ビットに、クエリベクトルは各次元を 4 ビットの int4 (0 から 15 の範囲)にスカラ量子化し、精度の向上を狙っています。BBQ ではクエリベクトルとデータベクトルの内積を最適化するため、クエリベクトルを 8 次元ごとにビットを並べ替えます。
ベンチマーク
PQ と BBQ を比較した結果が以下のブログで公開されています。
PQ と比較すると、BBQ はインデックス構築時間やレイテンシがかなり短く、精度 (recall) も僅かですが良いようです。
まとめ
この記事では、ANN でのベクトル量子化手法である RaBitQ と、Elasticsearch の BBQ (Better Binary Quantization) を紹介しました。
RaBitQ と BBQ の主な違いは、BBQ ではランダム射影 $P$ を使っていないという点です[20]。これはデータベクトルの分布によっては量子化誤差が大きくなってしまうことを意味し、誤差の上限を保証することもできません。論文の筆頭著者である Gao による以下の記事は、RaBitQ が高精度を達成できる直感的な理由が解説されています。
また、ANN を併用した BBQ ( bbq_hnsw )ではグラフベースアルゴリズムの HNSW を利用するため、誤差上限を利用したリランキングを利用することもできません(そもそも誤差上限の保証もありませんが)。
Elasticsearch の BBQ は、RaBitQ のランダム射影とリランキングを取り入れることで、さらに精度・速度の向上の余地がありそうです。
この記事は人力で書かれました。BBQ を利用する方の参考になれば幸いです。
Jianyang Gao and Cheng Long. 2024. RaBitQ: Quantizing High-Dimensional Vectors with a Theoretical Error Bound for Approximate Nearest Neighbor Search. Proc. ACM Manag. Data 2, 3, Article 167 (June 2024), 27 pages. https://doi.org/10.1145/3654970 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
松井 勇佑. 2019. 近似最近傍探索の最前線. MIRU 2019 チュートリアル. https://speakerdeck.com/matsui_528/jin-si-zui-jin-bang-tan-suo-falsezui-qian-xian ↩︎ ↩︎
Herve Jegou, Matthijs Douze, and Cordelia Schmid. 2011. Product Quantization for Nearest Neighbor Search. IEEE Trans. Pattern Anal. Mach. Intell. 33, 1 (January 2011), 117–128. https://doi.org/10.1109/TPAMI.2010.57 ↩︎ ↩︎ ↩︎
余談ですが、IVF での粗量子化器を HNSW にする手法もあります。 ↩︎
https://www.elastic.co/search-labs/blog/rabitq-explainer-101 ↩︎
実際には偏りがありますが、これをどのように解消するかを後で説明します。 ↩︎
https://www.elastic.co/search-labs/blog/rabitq-explainer-101 ↩︎
William B Johnson and Joram Lindenstrauss. 1984. Extensions of Lipschitz mappings into a Hilbert space. In: Proceedings of the 1982 Conference in Modern Analysis and Probability. Vol. 26. Contemporary Mathematics. AMS, 1984, pp. 189–206. https://doi.org/10.1090/conm/026/737400 ↩︎
Casper Benjamin Freksen. 2021. An introduction to Johnson-Lindenstrauss Transforms. arXiv [cs.DS]. Retrieved December 25, 2024 from http://arxiv.org/abs/2103.00564 ↩︎
Johnson-Lindenstraussの補題により、変換をしても2つのベクトルの距離が一定の誤差内に抑えられるという性質が証明されています(たとえ射影先が低次元でも)。 ↩︎
ランダム射影による特異値分解(次元削減)は、scikit-learn にも実装されています。 https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html#sklearn.decomposition.TruncatedSVD ↩︎
なお、データベクトルを正規化して $\bm{o}$ を計算するために $\bm{o_r}$ からセントロイド $\bm{c}$ を引いた後、ノルムで割って正規化していますが、実は量子化するうえではノルムで割らなくても同じ結果が得られます。RaBitQ でも BBQ でも、ノルムでの割り算は省略しています。 ↩︎
ランダム射影を使ったからだと思われる ↩︎
なお、この内積の値の保存はオプションです。保存しない場合、この値の理論値である 0.8 を使用することができます(Section 3.2.1)。 ↩︎
ここについては、実用上は確率的にサンプリングせず、四捨五入などで決定的に丸めるだけでも十分かもしれません。 ↩︎
https://www.elastic.co/search-labs/blog/better-binary-quantization-lucene-elasticsearch ↩︎ ↩︎ ↩︎
前の脚注で説明した通り、保存しない場合は理論値である 0.8 を使用します。 ↩︎
Jianyang Gao, Yutong Gou, Yuexuan Xu, Yongyi Yang, Cheng Long, and Raymond Chi-Wing Wong. 2024. Practical and asymptotically optimal quantization of high-dimensional vectors in Euclidean space for approximate nearest neighbor search. arXiv [cs.DB] http://arxiv.org/abs/2409.09913 ↩︎